جمع کننده با قابلیت پیش بینی بیت نقلی ( به انگلیسی: A carry - lookahead adder ) و به طور خلاصه CLA، نوعی مدار جمع کننده است که در مدارات منطقی به کار می رود. این مدار با کاهش زمان مورد نیاز برای تولید بیت نقلی سرعت جمع زدن را افزایش می دهد. در مقابل این نوع جمع کننده گونهٔ دیگری از مدار جمع کننده وجود دارد که با نام جمع کننده با بیت نقلی پله ای ( در بعضی متون ترجمه شده به فارسی جمع کننده با بیت نقلی موج گونه ) معروف است ( به انگلیسی: Ripple Carry Adder ) . هرچند که جمع کننده با بیت نقلی پله ای از لحاظ اجزای مداری ساده تراز جمع کننده با پیش بینی بیت نقلی می باشد اما از لحاظ سرعت انجام عملیات کندتر است چراکه در این گونه از جمع کننده ها مدار لازم است منتظر بماند تا بیت نقلی حاصل از جمع دو بیت قبلی محاسبه شده و آنگاه برای محاسبه بیت نقلی حاصل از جمع دو بیت بعدی اقدام کند. [ ۱] چارلز بابیج خطای تحمیل شده بر عملکرد مدار در اثر رقم نقلی پله ای را کشف کرد و در ماشین های محاسباتی خویش، ساز و کاری را جهت پیش بینی رقم نقلی توسعه داد. جرالد روزنبرگ از شرکت IBM حق اختراع یک جمع کننده دودویی با پیش بینی رقم نقلی را برای خود در سال ۱۹۵۷ ثبت نمود.
یک جمع کننده با بیت نقلی پله ای در جمع زدن از همان روشی استفاده می کند که یک انسان با استفاده از قلم و کاغذ انجام می دهد. از سمت راست ترین ( و در واقع کم ارزش ترین ) رقم شروع کرده و دو رقم متناظر با هم جمع می شوند و حاصل جمع بدست می آید. ممکن است که در این مرحله یک رقم نقلی نیز تولید شود ( به عنوان مثال در روش قلم و کاغذ حاصل جمع ۹ و ۵ برابر ۴ به همراه یک رقم نقلی ۱ خواهد بود ) . بر این اساس به غیر از سمت راست ترین موقعیت مکانی، دردیگر مکان های عددی باید رقم نقلی احتمالی ۱ که از سمت راست وارد می شود را نیز در محاسبه در نظر داشت. . این سخن بدین معناست که نمی توان مقدار نهایی حاصل جمع دو رقم در یک موقعیت مکانی را بدون دانستن اینکه آیا هیچگونه رقم نقلی از سمت راست وجود دارد یا نه، به طور قطع مشخص کرد. علاوه بر این چنانچه در روش قلم و کاغذ حاصل جمع بدون رقم نقلی ۹ بشود یا اینکه در محاسبات دودویی حاصل جمع بدون رقم نقلی برابر۱ بشود، حتی نمی توان گفت که آیا در آن موقعیت مکانی، باید یک رقم نقلی به سمت چپ منتقل بشود یا خیر. بدترین حالت هنگامی است که نتیجه جمع یک رشته رقم متناظر در سیستم دهگانی به شکل …۹۹۹۹۹. . . . یا در سیستم دودویی به شکل …۱۱۱۱. . . در بیاید، چراکه در اینصورت تا زمانی که مقدار رقم نقلی وارد شده از سمت راست، در دست نباشد به هیچ عنوان نمی توان نتیجه نهایی جمع را تعیین نمود و در واقع لازم است که رقم نقلی پس از هر بار ارزیابی به اندازه یک موقعیت مکانی به سمت چپ منتشر شود. به طور مثال در سیستم دهگانی اگر رقم نقلی برابر ۱ باشد نتیجه جمع دیگر ۹ نیست بلکه ۹+۱=۰ با نقلی جدید ۱ است یا در سیستم دودویی نتیجه جمع با احتساب نقلی ورودی دیگر ۱ نیست بلکه ۱+۱=۰ با نقلی خروجی ۱ است. علت نامگذاری جمع کننده های با بیت نقلی پله ای یا موج گونه به این نام آنست که در اینگونه جمع کننده ها، رقم نقلی مانند یک موج از راست به چپ منتشر می گردد که موجب کندی سرعت نیز می شود. به عنوان مثال در نظر بگیرید که بخواهید دو عدد صحیح ۳۲ بیتی را جمع بزنید در اینصورت رقم نقلی نهایی با عبور و انتشار رقم های نقلی پیشین از بین تمامی ۳۲ جمع کننده تک بیتی موجود در جمع کننده، تولید خواهد شد.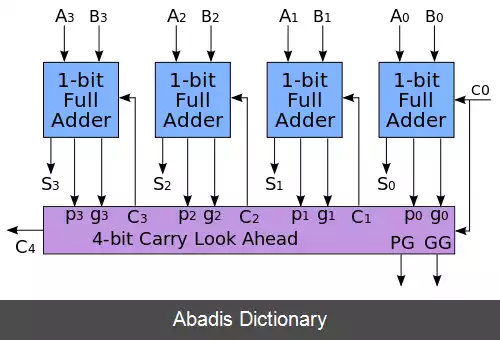
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک جمع کننده با بیت نقلی پله ای در جمع زدن از همان روشی استفاده می کند که یک انسان با استفاده از قلم و کاغذ انجام می دهد. از سمت راست ترین ( و در واقع کم ارزش ترین ) رقم شروع کرده و دو رقم متناظر با هم جمع می شوند و حاصل جمع بدست می آید. ممکن است که در این مرحله یک رقم نقلی نیز تولید شود ( به عنوان مثال در روش قلم و کاغذ حاصل جمع ۹ و ۵ برابر ۴ به همراه یک رقم نقلی ۱ خواهد بود ) . بر این اساس به غیر از سمت راست ترین موقعیت مکانی، دردیگر مکان های عددی باید رقم نقلی احتمالی ۱ که از سمت راست وارد می شود را نیز در محاسبه در نظر داشت. . این سخن بدین معناست که نمی توان مقدار نهایی حاصل جمع دو رقم در یک موقعیت مکانی را بدون دانستن اینکه آیا هیچگونه رقم نقلی از سمت راست وجود دارد یا نه، به طور قطع مشخص کرد. علاوه بر این چنانچه در روش قلم و کاغذ حاصل جمع بدون رقم نقلی ۹ بشود یا اینکه در محاسبات دودویی حاصل جمع بدون رقم نقلی برابر۱ بشود، حتی نمی توان گفت که آیا در آن موقعیت مکانی، باید یک رقم نقلی به سمت چپ منتقل بشود یا خیر. بدترین حالت هنگامی است که نتیجه جمع یک رشته رقم متناظر در سیستم دهگانی به شکل …۹۹۹۹۹. . . . یا در سیستم دودویی به شکل …۱۱۱۱. . . در بیاید، چراکه در اینصورت تا زمانی که مقدار رقم نقلی وارد شده از سمت راست، در دست نباشد به هیچ عنوان نمی توان نتیجه نهایی جمع را تعیین نمود و در واقع لازم است که رقم نقلی پس از هر بار ارزیابی به اندازه یک موقعیت مکانی به سمت چپ منتشر شود. به طور مثال در سیستم دهگانی اگر رقم نقلی برابر ۱ باشد نتیجه جمع دیگر ۹ نیست بلکه ۹+۱=۰ با نقلی جدید ۱ است یا در سیستم دودویی نتیجه جمع با احتساب نقلی ورودی دیگر ۱ نیست بلکه ۱+۱=۰ با نقلی خروجی ۱ است. علت نامگذاری جمع کننده های با بیت نقلی پله ای یا موج گونه به این نام آنست که در اینگونه جمع کننده ها، رقم نقلی مانند یک موج از راست به چپ منتشر می گردد که موجب کندی سرعت نیز می شود. به عنوان مثال در نظر بگیرید که بخواهید دو عدد صحیح ۳۲ بیتی را جمع بزنید در اینصورت رقم نقلی نهایی با عبور و انتشار رقم های نقلی پیشین از بین تمامی ۳۲ جمع کننده تک بیتی موجود در جمع کننده، تولید خواهد شد.

