در علوم کامپیوتر، یک جستجوی میبنیمم بازه ای ( Range minimum query ) الگوریتمی برای یافتن کوچکترین عنصر در یک زیر آرایه ( بازه ای از یک آرایه ) با عناصر قابل مقایسه است.
الگوریتم جستجوی مینیمم بازه ای در علوم و مهندسی کامپیوتر کاربردهای فراوانی دارند. از جمله آنان می توان به یافتن پایین ترین والد مشترک ( مثلا در درخت یا هرم یا … ) یا طولانی ترین پیشوند مشترک ( LCP ) اشاره کرد. ( لینک خارجی LCP array )
با توجه به یک آرایه [A[1 … n از n اشیاء از یک مجموعه منظم ( خوش ترتیب ) ( مانند اعداد ) ، جستجوی مینیمم بازه ای [RMQ A ( l, r ) =arg min A[k ( با ۱ ≤ l ≤ k ≤ r ≤ n ) موقعیت ( اندیس ) کوچکترین عنصر را در زیربازه ی مشخص شده [A[l … r بازمی گرداند.
به عنوان مثال ، وقتی A = ، آنگاه پاسخ به سؤال از دامنه A = برای زیر مجموعه A برابر است با ۷. زیرا A = ۱. و پاسخ، موقعیت کوچکترین عنصر در زیربازهٔ مشخص شده را به ما می دهد. ( البته اینجا اندیس ها را برای سادگی از یک شروع کردیم. اما در واقعیت از ۰ آغاز می شوند )
در یک مجموعه رایج، آرایه A استاتیک است، یعنی عناصر در طی یک سری پرس و جوها درج یا حذف نمی شوند؛ و جستجوهای داده شده باید به صورت درجا پاسخ داده شوند ( یعنی کل مجموعه نمایش داده ها از قبل با الگوریتم مشخص نیست ) در این حالت، پیش پردازش مناسب آرایه در یک داده ساختار، پاسخ سریع تر پرس و جو را تضمین می کند. یک راه حل ساده این است که پاسخ تمام جستجوهای ممکن را از قبل حساب کنیم، یعنی مینیمم تمام زیر مجموعه های A، و این موارد را در یک آرایه B ذخیره کنید به طوری که = min ( A[i…j ) ؛ سپس با استفاده از جستجوی آرایه در B یک جستجوی مینیمم در زمان ثابت حل می شود. تعداد ( Θ ( n² جستجوی مختلف روی آرایه ای به طول n وجود دارد، و پاسخ به این سوالات را می توان در زمان ( Θ ( n² توسط برنامه نویسی پویا بدست آورد.
مانند راه حل بالا، پاسخ دادن به این سؤالات در زمان ثابت با نتایج از پیش محاسباتی حاصل می شود. با این حال، این آرایه جستجوهای مینیمم از پیش محاسبه شده را برای محدوده هایی که اندازه آن ها توانی از ۲ است برای همه عناصر ذخیره می کند. برای هر موقعیت شروع i به تعداد ( Θ ( log n از این جستجوها وجود دارد، بنابراین اندازه جدول برنامه نویسی پویا B برابر با ( Θ ( n log n است. هر عنصر [B [i, j دارای اندیس مینیمم محدوده [A [i … i + 2^j - 1 است. جدول به کمک خاصیت بازگشت از اندیس های مینیمم ها پر شده است.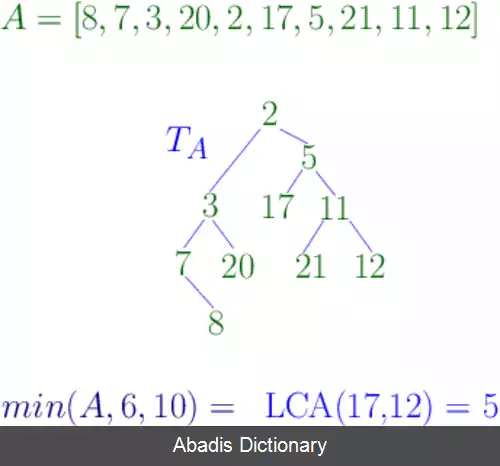
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفالگوریتم جستجوی مینیمم بازه ای در علوم و مهندسی کامپیوتر کاربردهای فراوانی دارند. از جمله آنان می توان به یافتن پایین ترین والد مشترک ( مثلا در درخت یا هرم یا … ) یا طولانی ترین پیشوند مشترک ( LCP ) اشاره کرد. ( لینک خارجی LCP array )
با توجه به یک آرایه [A[1 … n از n اشیاء از یک مجموعه منظم ( خوش ترتیب ) ( مانند اعداد ) ، جستجوی مینیمم بازه ای [RMQ A ( l, r ) =arg min A[k ( با ۱ ≤ l ≤ k ≤ r ≤ n ) موقعیت ( اندیس ) کوچکترین عنصر را در زیربازه ی مشخص شده [A[l … r بازمی گرداند.
به عنوان مثال ، وقتی A = ، آنگاه پاسخ به سؤال از دامنه A = برای زیر مجموعه A برابر است با ۷. زیرا A = ۱. و پاسخ، موقعیت کوچکترین عنصر در زیربازهٔ مشخص شده را به ما می دهد. ( البته اینجا اندیس ها را برای سادگی از یک شروع کردیم. اما در واقعیت از ۰ آغاز می شوند )
در یک مجموعه رایج، آرایه A استاتیک است، یعنی عناصر در طی یک سری پرس و جوها درج یا حذف نمی شوند؛ و جستجوهای داده شده باید به صورت درجا پاسخ داده شوند ( یعنی کل مجموعه نمایش داده ها از قبل با الگوریتم مشخص نیست ) در این حالت، پیش پردازش مناسب آرایه در یک داده ساختار، پاسخ سریع تر پرس و جو را تضمین می کند. یک راه حل ساده این است که پاسخ تمام جستجوهای ممکن را از قبل حساب کنیم، یعنی مینیمم تمام زیر مجموعه های A، و این موارد را در یک آرایه B ذخیره کنید به طوری که = min ( A[i…j ) ؛ سپس با استفاده از جستجوی آرایه در B یک جستجوی مینیمم در زمان ثابت حل می شود. تعداد ( Θ ( n² جستجوی مختلف روی آرایه ای به طول n وجود دارد، و پاسخ به این سوالات را می توان در زمان ( Θ ( n² توسط برنامه نویسی پویا بدست آورد.
مانند راه حل بالا، پاسخ دادن به این سؤالات در زمان ثابت با نتایج از پیش محاسباتی حاصل می شود. با این حال، این آرایه جستجوهای مینیمم از پیش محاسبه شده را برای محدوده هایی که اندازه آن ها توانی از ۲ است برای همه عناصر ذخیره می کند. برای هر موقعیت شروع i به تعداد ( Θ ( log n از این جستجوها وجود دارد، بنابراین اندازه جدول برنامه نویسی پویا B برابر با ( Θ ( n log n است. هر عنصر [B [i, j دارای اندیس مینیمم محدوده [A [i … i + 2^j - 1 است. جدول به کمک خاصیت بازگشت از اندیس های مینیمم ها پر شده است.


wiki: جستجوی مینیمم بازه ای
