در زمینه زیست شناسی محاسباتی، جستجوی دنباله موتیف کاشته شده ( PMS ) ، که با عنوان جست و جوی موتیف ( L، d ) نیز شناخته شده می شود، مسئله ی شناسایی توالی های حفظ شده در مجموعه ای از توالی های نوکلئیک اسید ( مانند توالی دی ان ای ) یا آمینواسید ( مانند توالی پروتئین ) می باشد.
پیدا کردن موتیف کاشته شده یک مسئله ی NP - کامل است. پیچیدگی زمانی اغلب الگوریتم های مطرح شده برای این مسئله، به صورت نمایی به مجموعه حروف الفبای مسئله و طول موتیف ( L ) بستگی دارد. مسئله ی PMS ابتدا توسط Keich و Pevzner و در سال 2002 معرفی شده است. [ ۱]
مسئله ی شناسایی الگوهای معنی دار ( از جمله موتیف ) از داده های بیولوژیکی به شدت مورد مطالعه قرار گرفته است، زیرا آنها نقش حیاتی در درک عملکرد ژن و بیماری های انسانی دارند و ممکن است به عنوان اهداف دارویی درمان قرار بگیرند.
نشانه های ریاضی به کاررفته در توصیف مسئله PMS، از قرار زیر است.
S = {s1, s2, s3, …, sn} رشته هایی هستند که در ورودی داده شده اند هر کدام از الفبای Σ تشکیل شده اند. به زیررشته هایی به طول L از هر کدام از این رشته ها، L - mer می گویند. در صورتی که a و b دو L - mer باشند، dH ( a, b ) را برابر فاصله همینگ بین a و b تعریف می کنیم. همجنین اگر s یکی از رشته هایی باشد که در ورودی داده شده است، dH ( a, s ) را برابر فاصله ی همینگ کمینه بین a و همه ی L - mer هایی مانند b از رشته ی s تعریف می کنیم. حال اگر S را برابر مجموعه ی همه ی رشته هایی بگیریم که در ورودی داده شده است، dH ( a, S ) را برابر maxsєSdH ( a, s ) تعریف می کنیم. همجنین با فرض اینکه u یک L - mer دلخواه باشد، d - همسایگی u را برابر مجموعه ی همه ی L - mer های v می گیریم که فاصله ی همینگ آن ها از u، کمتر و یا مساوی d باشد ( dH ( u, v ) ≤ d ) و آن را با Bd ( u ) نشان می دهیم. با فرض اینکه a و b دو L - mer دلخواه باشند، همه ی L - mer هایی که هم از x و هم از y ، فاصله ی همینگ کمتر و یا مساوی d دارند را با Bd ( x, y ) نشان می دهیم. این نمادگذاری قابل تعمیم برای بیشتر از دو L - mer نیز می باشد ( Bd ( x, y, z ) و . . . ) .
صورت مسئله ی جست و جوی موتیف به صورت خلاصه از قرار زیر است.
ورودی مسئله، شامل n رشته ی ( s1, s2, … , sn ) که هر کدام به طول m می باشد و از حروف الفبای Σ ایجاد شده اند. همچنین دو عدد طبیعی L و d نیز در ورودی داده می شود. همه ی رشته هایی مانند X به طول L را می خواهیم، به طوریکه هر کدام از رشته های ورودی، شامل یک زیررشته به طول L می باشند به طوریکه فاصله همینگ آن زیر رشته با X، حداکثر d باشد. هر کدام از این رشته های X، یک موتیف ( L، d ) نامیده می شوند. این مسئله معمولاً با عنوان جست و جوی موتیف ( L، d ) شناخته می شود. به عنوان مثال، با ورودی های GCGCGAT ، CACGTGA و CGGTGCC و همچنین d = 1 و L = 3 ، رشته ی GGT یک موتیف برای رشته ها می باشد. توجه شود که در رشته ی اول، زیررشته ی CGT، با فاصله همینگ 1 از موتیف GGT می باشد، همچنین در رشته ی دوم، GAT و در رشته ی سوم، GGT، نمونه های موتیف در رشته ها می باشند. معمولاً مسئله ی پیدا کردن موتیف، در توالی دی ان ای بررسی می شود، که در این حالت دارم: Σ ={G, C, T, A}. در صورتی هم که این مسئله در حوزه ی پروتئین بررسی شود، الفبای آن شامل 20 نوع اسیدآمینه می شود.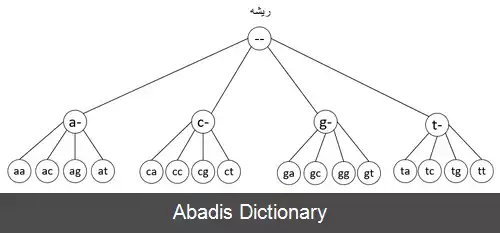
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفپیدا کردن موتیف کاشته شده یک مسئله ی NP - کامل است. پیچیدگی زمانی اغلب الگوریتم های مطرح شده برای این مسئله، به صورت نمایی به مجموعه حروف الفبای مسئله و طول موتیف ( L ) بستگی دارد. مسئله ی PMS ابتدا توسط Keich و Pevzner و در سال 2002 معرفی شده است. [ ۱]
مسئله ی شناسایی الگوهای معنی دار ( از جمله موتیف ) از داده های بیولوژیکی به شدت مورد مطالعه قرار گرفته است، زیرا آنها نقش حیاتی در درک عملکرد ژن و بیماری های انسانی دارند و ممکن است به عنوان اهداف دارویی درمان قرار بگیرند.
نشانه های ریاضی به کاررفته در توصیف مسئله PMS، از قرار زیر است.
S = {s1, s2, s3, …, sn} رشته هایی هستند که در ورودی داده شده اند هر کدام از الفبای Σ تشکیل شده اند. به زیررشته هایی به طول L از هر کدام از این رشته ها، L - mer می گویند. در صورتی که a و b دو L - mer باشند، dH ( a, b ) را برابر فاصله همینگ بین a و b تعریف می کنیم. همجنین اگر s یکی از رشته هایی باشد که در ورودی داده شده است، dH ( a, s ) را برابر فاصله ی همینگ کمینه بین a و همه ی L - mer هایی مانند b از رشته ی s تعریف می کنیم. حال اگر S را برابر مجموعه ی همه ی رشته هایی بگیریم که در ورودی داده شده است، dH ( a, S ) را برابر maxsєSdH ( a, s ) تعریف می کنیم. همجنین با فرض اینکه u یک L - mer دلخواه باشد، d - همسایگی u را برابر مجموعه ی همه ی L - mer های v می گیریم که فاصله ی همینگ آن ها از u، کمتر و یا مساوی d باشد ( dH ( u, v ) ≤ d ) و آن را با Bd ( u ) نشان می دهیم. با فرض اینکه a و b دو L - mer دلخواه باشند، همه ی L - mer هایی که هم از x و هم از y ، فاصله ی همینگ کمتر و یا مساوی d دارند را با Bd ( x, y ) نشان می دهیم. این نمادگذاری قابل تعمیم برای بیشتر از دو L - mer نیز می باشد ( Bd ( x, y, z ) و . . . ) .
صورت مسئله ی جست و جوی موتیف به صورت خلاصه از قرار زیر است.
ورودی مسئله، شامل n رشته ی ( s1, s2, … , sn ) که هر کدام به طول m می باشد و از حروف الفبای Σ ایجاد شده اند. همچنین دو عدد طبیعی L و d نیز در ورودی داده می شود. همه ی رشته هایی مانند X به طول L را می خواهیم، به طوریکه هر کدام از رشته های ورودی، شامل یک زیررشته به طول L می باشند به طوریکه فاصله همینگ آن زیر رشته با X، حداکثر d باشد. هر کدام از این رشته های X، یک موتیف ( L، d ) نامیده می شوند. این مسئله معمولاً با عنوان جست و جوی موتیف ( L، d ) شناخته می شود. به عنوان مثال، با ورودی های GCGCGAT ، CACGTGA و CGGTGCC و همچنین d = 1 و L = 3 ، رشته ی GGT یک موتیف برای رشته ها می باشد. توجه شود که در رشته ی اول، زیررشته ی CGT، با فاصله همینگ 1 از موتیف GGT می باشد، همچنین در رشته ی دوم، GAT و در رشته ی سوم، GGT، نمونه های موتیف در رشته ها می باشند. معمولاً مسئله ی پیدا کردن موتیف، در توالی دی ان ای بررسی می شود، که در این حالت دارم: Σ ={G, C, T, A}. در صورتی هم که این مسئله در حوزه ی پروتئین بررسی شود، الفبای آن شامل 20 نوع اسیدآمینه می شود.

wiki: جستجوی موتیف کاشته شده
