جستجوی درختی از جمله پرکاربردترین استفاده از یک درخت است. درخت یک مدل مناسب برای نمایش بسیاری از مفاهیم، پدیده ها و رابطهٔ بین آن هاست. مثلاً درخت فامیلی، سلسله مراتب اداری، عبارات ریاضی و بسیاری از بازی ها با درخت مدل می شوند. در واقع درخت ها، گراف های خاصی هستند که در مورد ویژگی های آن ها نتایج نظری زیادی وجود دارد. [ ۱]
درخت ها بسته به نوع نیاز، تعداد برگ های مختلفی دارند. الگوریتم جستجو مختص به تعداد برگ های درخت می باشد که عبارتند از:درخت جستجوی سه تایی ، درخت جستجوی دودویی خود - متوازن ، درخت جستجوی دودویی متوازن وزن دار ، درخت جستجوی تعمیم یافته، درخت جستجو بندانگشتی و. . . در اینجا سه نوع جستجوی رایج را در درخت دودویی و درخت با تعداد برگ نامشخص و ترای ( همان درخت پیشوندی است که برای جستجوی رشته ای مناسب است ) بررسی می کنیم.
درخت دودویی درخت مرتبی است که هر عنصر آن حداکثر دارای دو فرزند چپ و راست باشد. اگر یک گره فقط یک فرزند داشته باشد، باید مشخص شود که فرزند چپ است یا راست. درخت عبارت و درخت تصمیم نمونه هایی از کاربردهای درخت دودویی هستند. [ ۱]
معروف به د. د. ج می باشد. معمولاً عملیات زیر بر روی یک درخت جستجوی دودویی تعریف می شود:
• ایجاد یک درخت جستجوی خالی
• آزمایش خالی بودن درخت
• درج کردن یک کلید جدید در درخت، بدون برهم خوردن خاصیت درخت
• جستجو کردن و یافتن یک کلید خاص در درخت
• حذف کردن یک کلید از درخت، با حفظ خاصیت درخت
• پیمایش درخت جستجوی دودویی، به طوری تمام گره ها دقیقاً یک بار مورد دسترسی قرارگیرند.
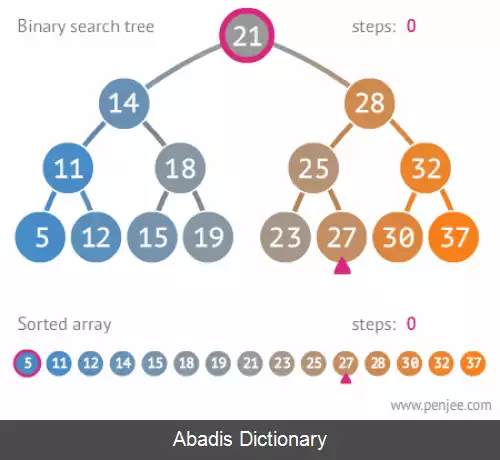
برای پیدا کردن گرهی با یک کلید خاص مانند key در درخت، ابتدا باید از ریشه درخت شروع کنیم. اگر ریشه تهی باشد، درخت فاقد هر عنصری بوده و جستجو ناموفق خواهد بود. در غیر اینصورت، key را با مقدار گره ریشه مقایسه می کنیم، اگر برابر بودند، جستجو موفق است و گره ریشه همان گره موردنظر است. در غیر این صورت، دو حالت پیش خواهدآمد:
• key از گره ریشه کوچکتر است. در این حالت، هیچ عنصری در زیردرخت سمت راست وجود ندارد که مقدار کلید آن برابر با key باشد؛ بنابراین جستجو باید در زیردرخت سمت چپ ادامه یابد.
• key بزرگتر از گره ریشه است. در این حالت، هیچ عنصری در زیردرخت سمت چپ وجود ندارد که مقدار کلید آن برابر با key باشد؛ بنابراین جستجو باید در زیردرخت سمت راست ادامه یابد.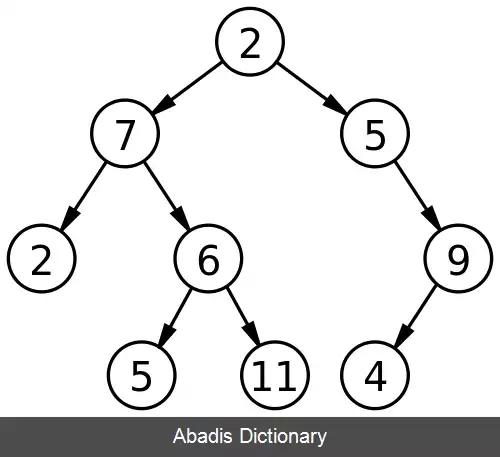
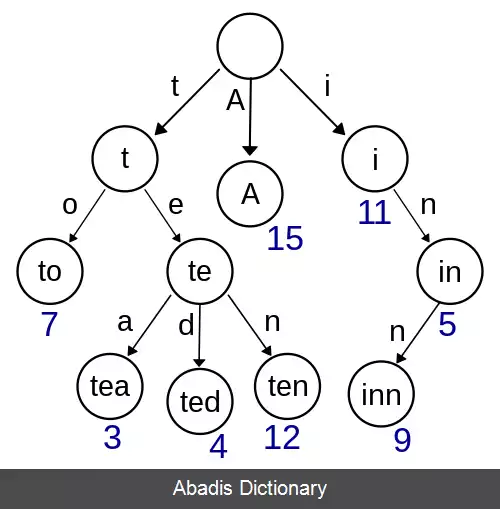
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدرخت ها بسته به نوع نیاز، تعداد برگ های مختلفی دارند. الگوریتم جستجو مختص به تعداد برگ های درخت می باشد که عبارتند از:درخت جستجوی سه تایی ، درخت جستجوی دودویی خود - متوازن ، درخت جستجوی دودویی متوازن وزن دار ، درخت جستجوی تعمیم یافته، درخت جستجو بندانگشتی و. . . در اینجا سه نوع جستجوی رایج را در درخت دودویی و درخت با تعداد برگ نامشخص و ترای ( همان درخت پیشوندی است که برای جستجوی رشته ای مناسب است ) بررسی می کنیم.
درخت دودویی درخت مرتبی است که هر عنصر آن حداکثر دارای دو فرزند چپ و راست باشد. اگر یک گره فقط یک فرزند داشته باشد، باید مشخص شود که فرزند چپ است یا راست. درخت عبارت و درخت تصمیم نمونه هایی از کاربردهای درخت دودویی هستند. [ ۱]
معروف به د. د. ج می باشد. معمولاً عملیات زیر بر روی یک درخت جستجوی دودویی تعریف می شود:
• ایجاد یک درخت جستجوی خالی
• آزمایش خالی بودن درخت
• درج کردن یک کلید جدید در درخت، بدون برهم خوردن خاصیت درخت
• جستجو کردن و یافتن یک کلید خاص در درخت
• حذف کردن یک کلید از درخت، با حفظ خاصیت درخت
• پیمایش درخت جستجوی دودویی، به طوری تمام گره ها دقیقاً یک بار مورد دسترسی قرارگیرند.
برای پیدا کردن گرهی با یک کلید خاص مانند key در درخت، ابتدا باید از ریشه درخت شروع کنیم. اگر ریشه تهی باشد، درخت فاقد هر عنصری بوده و جستجو ناموفق خواهد بود. در غیر اینصورت، key را با مقدار گره ریشه مقایسه می کنیم، اگر برابر بودند، جستجو موفق است و گره ریشه همان گره موردنظر است. در غیر این صورت، دو حالت پیش خواهدآمد:
• key از گره ریشه کوچکتر است. در این حالت، هیچ عنصری در زیردرخت سمت راست وجود ندارد که مقدار کلید آن برابر با key باشد؛ بنابراین جستجو باید در زیردرخت سمت چپ ادامه یابد.
• key بزرگتر از گره ریشه است. در این حالت، هیچ عنصری در زیردرخت سمت چپ وجود ندارد که مقدار کلید آن برابر با key باشد؛ بنابراین جستجو باید در زیردرخت سمت راست ادامه یابد.



wiki: جستجوی درختی
