از جریمه های پرش برای هم ترازسازی توالی استفاده می شود. جریمه های پرش به محاسبهٔ کلی امتیاز تطابق ها کمک می کنند، و بنابراین، نسبت اندازهٔ جریمهٔ پرش به تعداد درایه های ماتریس شباهت ( similarity matrix ) تطابقی که نهایتاً انتخاب می شود را تحت تأثیر قرار می دهد.
جریمهٔ پرش ثابت از ساده ترین مدل های جریمهٔ پرش است. در این روش زمانی که یک پرش برای اولین بار در توالی به کار گرفته می شود فقط یک پارامتر d، به امتیاز تطابق اضافه می شود و این بدین معناست که هر پرش یک جریمهٔ یکسان دریافت می کند، مستقل از اینکه این پرش دارای چه اندازه ایست.
جریمهٔ پرش خطی فقط یک پارامترِ d دارد که معرف جریمه در واحد طول پرش است. این مقدار در اکثر مواقع مقداری منفی است، بنابراین تطابق با تعداد پرش های کمتر بهتر است از تطابق با پرش های بیشتر. در روش جریمهٔ پرش خطی، جریمهٔ کلی برای یک پرش بزرگ همانند جریمهٔ کلی برای چندین پرش کوچک است.
در برخی توالی ها بیشتر این احتمال وجود دارد که یک پرش بزرگ داشته باشیم به جای چندین پرش کوچک. برای مثال رخ دادن یک پرش به طول دو محتمل تر از حالت دیگر است. این تفاوت در هنگام استفاده از جریمهٔ پرش نسبی، لحاظ می شود، ولی در سایر سیاست های پرش، هر دو حالت یک امتیاز می گیرند. این جریمه به صورت σ + ( L - 1 ) . ε مدل می شود، که در آن σ ، جریمهٔ اولین پرش ( gap opening penalty ) با هر طولی می باشد. ε ، جریمهٔ امتداد پرش های ( gap extension penalty ) ایجاد شده به طول ۱ می باشد. L هم تعداد کل پرش ها می باشد. به طور مثال، در صورتی که ۵ پرش پشت سر هم رخ دهند، جریمهٔ آن به صورت σ + 4ε مدل می شود. [ ۱] معمولاً معیار خاصی برای تعیین کردن مقادیر ε و σ وجود ندارد و این مقادیر با توجه به هدف ما از هم ترازسازی توالی ها تفاوت می کنند. معمولاً هنگامی که به دنبال دنباله های نزدیک به هم هستیم، مقدار جریمهٔ ایجاد شکاف ( σ ) ، نسبتاً بزرگتر از زمانی است که دنبال رشته های متفاوت از هم می باشیم. [ ۲] الگوریتم هایی برای هم ترازسازی توالی ها با استفاده از این جریمه وجود دارند که دو نمونه از آن ها که زمان اجرای متفاوتی دارند، در زیر بررسی می شوند.
برای هم ترازسازی توالی ها، روش هایی بر مبنای برنامه ریزی پویا معرفی شده اند که از معروف ترین آن ها، الگوریتم نیدلمن - وانچ می باشد. برای هم تراز سازی توالی ها با استفاده از جریمهٔ پرش نسبی، از الگوریتمی مانند الگوریتم نیدلمن - وانچ استفاده می کند. بدین صورت که گراف ویرایش ( edit graph ) را بدین صورت تغییر می دهد که یال های عمودی و افقی میان رأس ها و رأس های بعدیشان اضافه می کنیم، به طوری که هر یال به طول x، وزن σ + ( ε - 1 ) . x داشته باشد. با اضافه کردن این یال ها، زمان اجرای الگوریتم از ( O ( n2 به ( O ( n3 افزایش می دهد.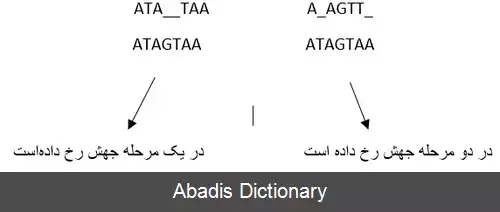
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفجریمهٔ پرش ثابت از ساده ترین مدل های جریمهٔ پرش است. در این روش زمانی که یک پرش برای اولین بار در توالی به کار گرفته می شود فقط یک پارامتر d، به امتیاز تطابق اضافه می شود و این بدین معناست که هر پرش یک جریمهٔ یکسان دریافت می کند، مستقل از اینکه این پرش دارای چه اندازه ایست.
جریمهٔ پرش خطی فقط یک پارامترِ d دارد که معرف جریمه در واحد طول پرش است. این مقدار در اکثر مواقع مقداری منفی است، بنابراین تطابق با تعداد پرش های کمتر بهتر است از تطابق با پرش های بیشتر. در روش جریمهٔ پرش خطی، جریمهٔ کلی برای یک پرش بزرگ همانند جریمهٔ کلی برای چندین پرش کوچک است.
در برخی توالی ها بیشتر این احتمال وجود دارد که یک پرش بزرگ داشته باشیم به جای چندین پرش کوچک. برای مثال رخ دادن یک پرش به طول دو محتمل تر از حالت دیگر است. این تفاوت در هنگام استفاده از جریمهٔ پرش نسبی، لحاظ می شود، ولی در سایر سیاست های پرش، هر دو حالت یک امتیاز می گیرند. این جریمه به صورت σ + ( L - 1 ) . ε مدل می شود، که در آن σ ، جریمهٔ اولین پرش ( gap opening penalty ) با هر طولی می باشد. ε ، جریمهٔ امتداد پرش های ( gap extension penalty ) ایجاد شده به طول ۱ می باشد. L هم تعداد کل پرش ها می باشد. به طور مثال، در صورتی که ۵ پرش پشت سر هم رخ دهند، جریمهٔ آن به صورت σ + 4ε مدل می شود. [ ۱] معمولاً معیار خاصی برای تعیین کردن مقادیر ε و σ وجود ندارد و این مقادیر با توجه به هدف ما از هم ترازسازی توالی ها تفاوت می کنند. معمولاً هنگامی که به دنبال دنباله های نزدیک به هم هستیم، مقدار جریمهٔ ایجاد شکاف ( σ ) ، نسبتاً بزرگتر از زمانی است که دنبال رشته های متفاوت از هم می باشیم. [ ۲] الگوریتم هایی برای هم ترازسازی توالی ها با استفاده از این جریمه وجود دارند که دو نمونه از آن ها که زمان اجرای متفاوتی دارند، در زیر بررسی می شوند.
برای هم ترازسازی توالی ها، روش هایی بر مبنای برنامه ریزی پویا معرفی شده اند که از معروف ترین آن ها، الگوریتم نیدلمن - وانچ می باشد. برای هم تراز سازی توالی ها با استفاده از جریمهٔ پرش نسبی، از الگوریتمی مانند الگوریتم نیدلمن - وانچ استفاده می کند. بدین صورت که گراف ویرایش ( edit graph ) را بدین صورت تغییر می دهد که یال های عمودی و افقی میان رأس ها و رأس های بعدیشان اضافه می کنیم، به طوری که هر یال به طول x، وزن σ + ( ε - 1 ) . x داشته باشد. با اضافه کردن این یال ها، زمان اجرای الگوریتم از ( O ( n2 به ( O ( n3 افزایش می دهد.

wiki: جریمه پرش
