جانشینی مثلثاتی ( به انگلیسی: Trigonometric substitution ) در ریاضیات و در محاسبه انتگرال توابع به منظور ساده تر کردن توابع به کار می رود. مثلاً برای تبدیل عبارات رادیکالی و نمایی می توان از این تبدیل ها استفاده کرد[ ۱] [ ۲] .
• اگر انتگرال شامل عبارت a2 − x2 باشد:
و از اتحاد مثلثاتی زیر استفاده می کنیم:
• اگر انتگرال شامل عبارت a2 + x2, باشد:
• گر انتگرال شامل عبارت x2 − a2, باشد:
انتگرال های شامل g a2 − x2 در انتگرال زیر:
می توان از روابط مثلثاتی زیر استفاده کرد:
باید توجه داشت که در نمونه فوق باید همواره a> 0
نکته دیگر تغییر حدود انتگرال برای انتگرال های معین است. مثلاً اگر x از 0 تا a/2 تغییر کند، sin ( θ ) از 0 تا 1/2 تغییر می کند ، در نتیجه θ از 0 تا π/6 تغییر می کند: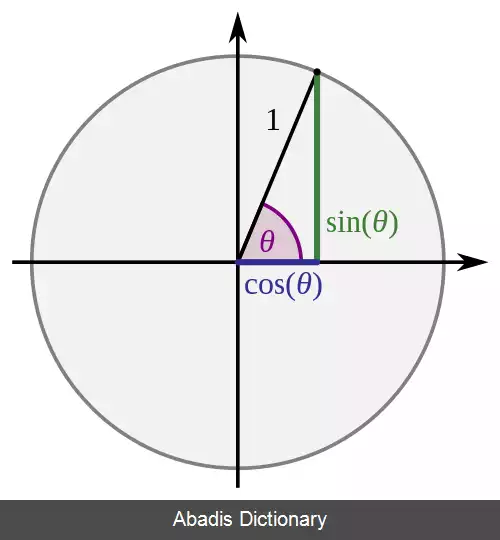
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• اگر انتگرال شامل عبارت a2 − x2 باشد:
و از اتحاد مثلثاتی زیر استفاده می کنیم:
• اگر انتگرال شامل عبارت a2 + x2, باشد:
• گر انتگرال شامل عبارت x2 − a2, باشد:
انتگرال های شامل g a2 − x2 در انتگرال زیر:
می توان از روابط مثلثاتی زیر استفاده کرد:
باید توجه داشت که در نمونه فوق باید همواره a> 0
نکته دیگر تغییر حدود انتگرال برای انتگرال های معین است. مثلاً اگر x از 0 تا a/2 تغییر کند، sin ( θ ) از 0 تا 1/2 تغییر می کند ، در نتیجه θ از 0 تا π/6 تغییر می کند:

wiki: جانشینی مثلثاتی
