در ریاضیات ترکیبیاتی، جابه جایی چرخشی یا جابه جایی دَوَرانی یا شیفت دوری عملیاتی است که درایه های یک چندتایی را با حرکت دادن درایه انتهایی به موقعیت آغازین آن، مجدداً آرایش می دهد، در حالی که تمام درایه های دیگر به مکان بعدی خود نقل مکان می کنند، یا با عملی معکوس با آنچه توصیف شد، در جهت مخالف جابه جایی آرایه ها صورت می پذیرد. جابه جایی دورانی نوع خاصی از جایگشت دوری است که به نوبه خود نوع خاصی از جایگشت است. به طور صوری، جابه جایی دورانی را می توان جایگشتی چون σ از n عنصر در نظر گرفت که در یک چندتایی قرار دارند چنان که برای تمام i = 1 , ⋯ , n به پیمانه n داریم:
یا:
برای نمونه، با اعمال جابه جایی دورانی به طور مکرر روی چندتایی چهارتایی ( a , b , c , d ) به صورت پشت سر هم به نتایج زیر می رسیم:
• ( d, a, b, c ) ,
• ( c, d, a, b ) ,
• ( b, c, d, a ) ,
• ( a, b, c, d )
که تاپل آخر، همان تاپل اولیه ما می باشد.
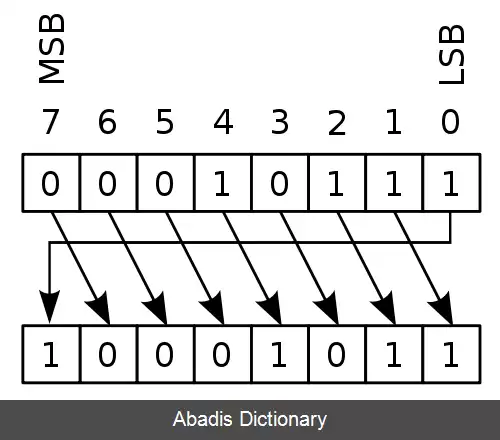
اگر دنباله بیتی 00010111 تحت جابه جایی دورانی تک بیتی قرار بگیرد … ( تصاویر زیر را ببینید ) :
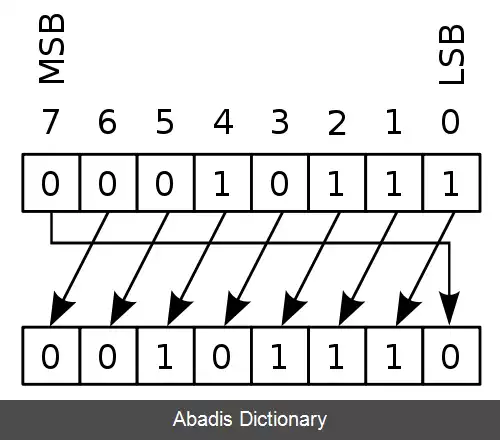
اگر دنباله بیتی 10010110 تحت عملیات زیر قرار می گرفت: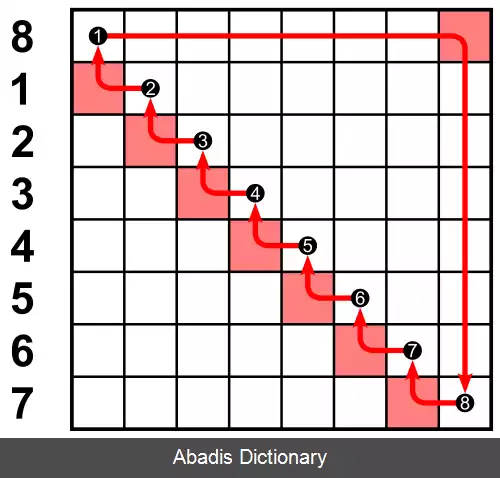

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیا:
برای نمونه، با اعمال جابه جایی دورانی به طور مکرر روی چندتایی چهارتایی ( a , b , c , d ) به صورت پشت سر هم به نتایج زیر می رسیم:
• ( d, a, b, c ) ,
• ( c, d, a, b ) ,
• ( b, c, d, a ) ,
• ( a, b, c, d )
که تاپل آخر، همان تاپل اولیه ما می باشد.
اگر دنباله بیتی 00010111 تحت جابه جایی دورانی تک بیتی قرار بگیرد … ( تصاویر زیر را ببینید ) :
اگر دنباله بیتی 10010110 تحت عملیات زیر قرار می گرفت:




wiki: جابه جایی چرخشی
