جابه جایی لمب

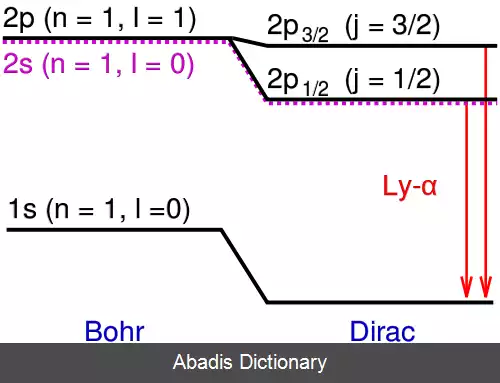
در دانش فیزیک، تغییر لمب که نام آن از نام ویلیس اوژن لمب، فیزیکدان آمریکایی ( ۱۹۱۳ - ۲۰۰۸ ) گرفته شده است، به اختلاف اندکی در میزان انرژی بین دو تراز انرژی 2S1/2 و 2P1/2 ازاتم هیدروژن در الکترودینامیک کوانتومی ( QED ) است. بنا بر معادله دیراک، اوربیتال های 2S1/2 و 2P1/2 باید انرژی یکسانی داشته باشند، اما برهم کنش میان الکترون و خلاء ( که در معادله دیراک نادیده گرفته شده است. ) باعث تغییری اندک در میزان انرژی می شود که مقدارش برای 2S1/2 و 2P1/2 متفاوت است. لمب و رابرت رادرفورد این تغییر را در سال ۱۹۴۷ اندازه گرفتند[ ۱] و این اندازه گیری انگیزه ای برای بازبه هنجارسازی نظریه شد تا همه واگرایی ها را نیز دربربگیرد. این موضوع زمینه ساز پیدایش الکترودینامیک کوانتومی نوین توسطجولیان شوینگر، ریچارد فاینمن، ارنست اشتوکلبرگ وسین ایترو تومونوجا شد. لمب در سال ۱۹۵۵ به خاطر کشفیات مربوط به تغییر لمب، مفتخر به دریافت جایزه نوبل فیزیک شد.
این روش ابتکاری برای نتیجه گیری تغییر در تراز الکترودینامیکی از نورشناسی کوانتومی گرفته شده است. [ ۲]
نوسان در میدان های الکتریکی و مغناطیسی مرتبط به خلاء الکترودینامیکی پتانسیل الکتریکی ناشی از هسته اتم را دچار اغتشاش می کند. این اغتشاش به نوسان در موقعیت الکترون می انجامد که تغییر در انرژی آن را توضیح می دهد. اختلاف در انرژی پتانسیل از رابطه زیر به دست می آید:
از آنجا که نوسانات همسانگرد هستند،
پس رابطه زیر به دست می آید:
معادله کلاسیک حرکت برای جابجایی الکترون ( δr ) k→ القا شده توسط یک مود تکی میدان بردار موج k→ و بسامد v عبارت است از:
واین تنها در صورتی برقرار است که بسامد v بزرگتر از ν0 در مدار بور باشد، ν> πc/a0. اگر نوسان ها کوچکتر از بسامد طبیعی اوربیتال در اتم باشد، الکترون قادر به پاسخ به میدان در حال نوسان نخواهد بود.
برای میدان در حال نوسان با بسامد v:
پس؛
با محاسبه مجموع روی کل k → ،
که در آن Ω حجم یک به هنجارسازی بزرگ است ( حجم یک جعبه فرضی شامل اتم هیدروژن ) و
به دلیل پیوستگی k→, ∑ k → → 2 Ω ( 2 π ) 3 ∫ d 3 k مجموع به انتگرال تبدیل می شود، به گونه ای که
این نتیجه بدون حدی روی انتگرال، واگراست. همان طور که در بالا عنوان شد این روش تنها زمانی اعتبار دارد که ν> πc/a0 یا به عبارتی k> π/a0. همچنین تنها در صورتی معتبر است که طول موج ها از طول موج کامپتون بزرگتر باشد یا به عبارتی k < mc/ħ. بدین ترتیب می توانیم حدود بالا و پایین برای انتگرال را به دست آوریم و این حدود باعث همگرایی جواب می شوند.