در نگرش ( نظریه ) آمار و احتمال، توزیع یکنواخت پیوسته یا توضیح راست گوشه از هم شاخه های توزیع های احتمال متقارن است. همچنین طول تمام فواصل هر عضو شاخه تحت این توزیع احتمال یکسان است. کران ( support ) با دو مقدار a و b که کمینه و بیشینه هستند تعریف می شود. شکل مختصر توزیع اغلب ( U ( a, b چنین است.
تابع تابع چگالی احتمال یک توزیع یکنواخت پیوسته چنین می باشد.
مقدار f ( x ) در کران معمولاً مهم نیست، زیرا مقدار انتگرال f ( x ) d x در هر فاصله ای بدون تغییر ( ثابت ) می ماند؛ و نه x f ( x ) d x و نه هر مرتبه بالاتری. بسته به مکان متغیر x گاهی مقدار تابع صفر و گاهی 1 b − a . در حالت دوم در زمینه برآورد به روش حداکثر احتمال مناسب است. در آنالیز فوریه، یکی ممکن است مقدار f ( a ) یا f ( b ) که 1 2 ( b − a ) باشد را بردارد. تبدیل معکوس بسیاری از تبدیل های انتگرالی این تابع یکنواخت به شکل خودش است. ( به عبارتی تصویر خودش است )
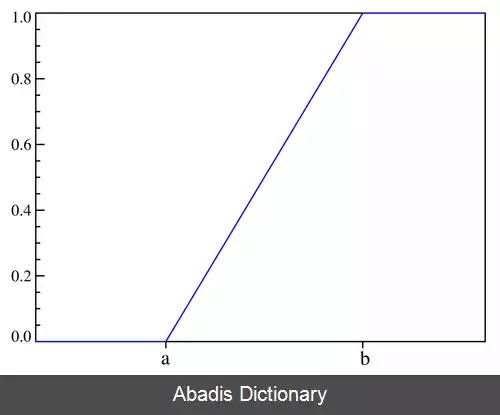
F ( x ) = { 1 2 σ 3 for − σ 3 ≤ x − μ ≤ σ 3 0 otherwise
F − 1 ( p ) = σ 3 ( 2 p − 1 ) + μ for 0 ≤ p ≤ 1 تابع مولد تابع مولد گشتاور تابع مولد گشتاور چنین است.
هر گاه a = 0 و b = 1 باشد، آنگاه توزیع یکنواخت پیوسته را توزیع یکنواخت پیوسته استاندارد گویند.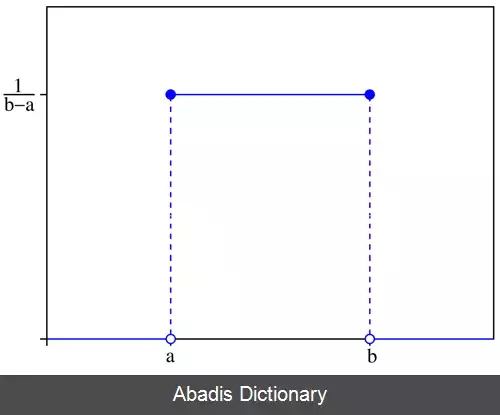
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتابع تابع چگالی احتمال یک توزیع یکنواخت پیوسته چنین می باشد.
مقدار f ( x ) در کران معمولاً مهم نیست، زیرا مقدار انتگرال f ( x ) d x در هر فاصله ای بدون تغییر ( ثابت ) می ماند؛ و نه x f ( x ) d x و نه هر مرتبه بالاتری. بسته به مکان متغیر x گاهی مقدار تابع صفر و گاهی 1 b − a . در حالت دوم در زمینه برآورد به روش حداکثر احتمال مناسب است. در آنالیز فوریه، یکی ممکن است مقدار f ( a ) یا f ( b ) که 1 2 ( b − a ) باشد را بردارد. تبدیل معکوس بسیاری از تبدیل های انتگرالی این تابع یکنواخت به شکل خودش است. ( به عبارتی تصویر خودش است )
F ( x ) = { 1 2 σ 3 for − σ 3 ≤ x − μ ≤ σ 3 0 otherwise
F − 1 ( p ) = σ 3 ( 2 p − 1 ) + μ for 0 ≤ p ≤ 1 تابع مولد تابع مولد گشتاور تابع مولد گشتاور چنین است.
هر گاه a = 0 و b = 1 باشد، آنگاه توزیع یکنواخت پیوسته را توزیع یکنواخت پیوسته استاندارد گویند.


wiki: توزیع یکنواخت پیوسته
