در علم احتمالات و آمار، توزیع گمپرتز ( Gompertz distribution ) یک توزیع احتمال پیوسته است که به بزرگداشت بنجامین گمپرتز ( ۱۸۶۵–۱۷۷۹ ) چنین نامگذاری شده است. این توزیع برای توصیفِ توزیع بازهٔ زندگی بزرگسالان با کمک جمعیت شناسی[ ۱] [ ۲] و مرگر[ ۳] [ ۴] می پردازد. زمینه های دیگر مرتبط علمی مانند زیست شناسی[ ۵] و پیری شناسی[ ۶] نیز از توزیع گمپرتز برای تحلیل به جای ماندگان ( زنده ها ) استفاده می کنند. به تازگی در علوم رایانه برای مدل سازی نرخ شکست کدهای رایانه ای از توزیع گمپرتز استفاده می شود. [ ۷] همچنین در علم بازاریابی هم این توزیع برای شبیه سازی مدل ارزش طول عمر مشتری کاربرد دارد. [ ۸]
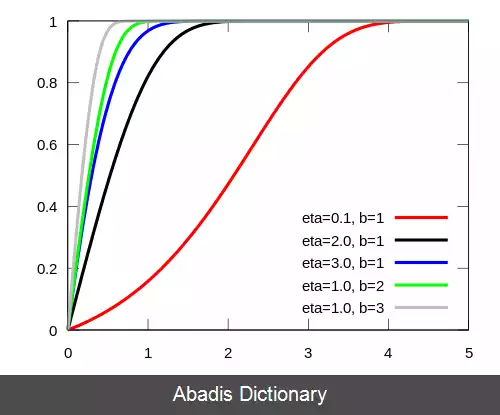
توزیع گمپرتز، یک توزیع انعطاف پذیر است و ممکن است به راست یا چپ متمایل شود، تابع شکست آن یک تابع محدب F ( x ; η , b ) است.
تابع چگالی گمپرتز بسته به مقدارهای مختلف پارامتر شکلی η می تواند شکل های مختلف به خود بگیرد:
• هرگاه η ≥ 1 , {\displaystyle \eta \geq 1, \, } باشد، مُد تابع چگالی احتمالاتی در صفر خواهد بود.
• هرگاه 0 < η < 1 , {\displaystyle 0< \eta < 1, \, } مد تابع چگالی احتمالاتی به صورت زیر خواهد بود:
هرگاه f 1 و f 2 تابع های چگالی احتمالاتی دو توزیع گمپرتز باشند آنگاه واگرایی کولبک - لیبلر به صورت زیر خواهد بود:
در رابطهٔ بالا، Γ ( ⋅ , ⋅ ) تابع گامای ناکامل بالایی و Ei ( ⋅ ) انتگرال نمایی است. [ ۹]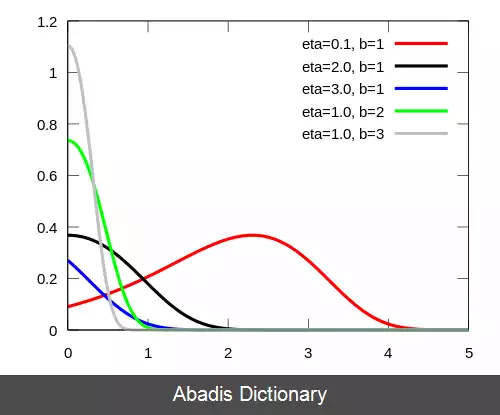
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتوزیع گمپرتز، یک توزیع انعطاف پذیر است و ممکن است به راست یا چپ متمایل شود، تابع شکست آن یک تابع محدب F ( x ; η , b ) است.
تابع چگالی گمپرتز بسته به مقدارهای مختلف پارامتر شکلی η می تواند شکل های مختلف به خود بگیرد:
• هرگاه η ≥ 1 , {\displaystyle \eta \geq 1, \, } باشد، مُد تابع چگالی احتمالاتی در صفر خواهد بود.
• هرگاه 0 < η < 1 , {\displaystyle 0< \eta < 1, \, } مد تابع چگالی احتمالاتی به صورت زیر خواهد بود:
هرگاه f 1 و f 2 تابع های چگالی احتمالاتی دو توزیع گمپرتز باشند آنگاه واگرایی کولبک - لیبلر به صورت زیر خواهد بود:
در رابطهٔ بالا، Γ ( ⋅ , ⋅ ) تابع گامای ناکامل بالایی و Ei ( ⋅ ) انتگرال نمایی است. [ ۹]


wiki: توزیع گمپرتز
