توزیع گاوسی معکوس تعمیم یافته ( GIG : Generalized Inverse Gaussian ) در نظریه احتمال و آمار یک توزیع پیوسته با سه پارامتر است. تابع چگالی احتمال این توزیع به صورت زیر است:
بارندورف - نیلسن ( O. Barndorff - Nielsen ) و هالگرین ( C. Halgreen ) اثبات کردند که توزیع GIG بی نهایت تقسیم پذیر است. [ ۱]
آنتروپی توزیع GIG به صورت زیر داده میشود:
H = 1 2 log ( b a ) + log ( 2 K p ( a b ) ) − ( p − 1 ) ν = p K p ( a b ) + a b 2 K p ( a b ) ( K p + 1 ( a b ) + K p − 1 ( a b ) )
توزیع گاوسی معکوس و توزیع گاما حالت های خاصی از توزیع گاوسی معکوس تعمیم یافته با p = − 1 / 2 و b = 0 هستند. [ ۲]
به طور دقیق ، یک توزیع گاوسی معکوس با فرم
f ( x ; μ , λ ) = 1 / 2 exp − λ ( x − μ ) 2 2 μ 2 x
یک توزیع گاوسی معکوس تعمیم یافته با a = λ / μ 2 ، b = λ و p = − 1 / 2 است.
یک توزیع گاما با فرم
g ( x ; α , β ) = β α 1 Γ ( α ) x α − 1 e − β x
یک توزیع گاوسی معکوس تعمیم یافته با a = 2 β ، b = 0 و p = α است.
یک توزیع گاما معکوس، یک توزیع گاوسی معکوس تعمیم یافته با a = 0 و p < 0 است. [ ۳]
یک توزیع هایپربولیک، یک توزیع گاوسی معکوس تعمیم یافته با p = 0 است. [ ۲]
X و Y را دو متغیر تصادفی مستقل از هم در نظر بگیرید به طوری که X > 0 و Y ∼ γ ( p , a 2 ) برای p , a > 0 . در این صورت داریم X = d 1 Y + X اگر و فقط اگر X ∼ G I G ( − p , a , a ) .
X ، Y 1 و Y 2 را سه متغیر تصادفی مستقل از هم در نظر بگیرید به طوری که X > 0 ، Y 1 ∼ γ ( p , b 2 ) و Y 2 ∼ γ ( p , a 2 ) برای p , a , b > 0 . در این صورت داریم X = d 1 Y 1 + 1 Y 2 + X اگر و فقط اگر X ∼ G I G ( − p , a , b ) .
به طور کلی اگر ( Y i ) i ≥ 1 یک دنباله از متغیر تصادفی های مستقل از هم باشد به طوری که L ( Y 2 i − 1 ) = L ( Y 1 ) = γ ( λ , b 2 ) و L ( Y 2 i ) = L ( Y 2 ) = γ ( λ , a 2 ) برای i ≥ 1 ، آنگاه داریم: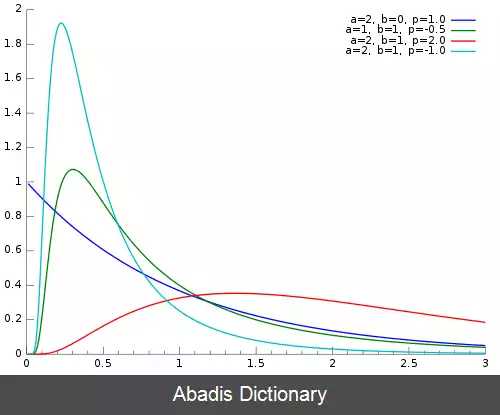
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبارندورف - نیلسن ( O. Barndorff - Nielsen ) و هالگرین ( C. Halgreen ) اثبات کردند که توزیع GIG بی نهایت تقسیم پذیر است. [ ۱]
آنتروپی توزیع GIG به صورت زیر داده میشود:
H = 1 2 log ( b a ) + log ( 2 K p ( a b ) ) − ( p − 1 ) ν = p K p ( a b ) + a b 2 K p ( a b ) ( K p + 1 ( a b ) + K p − 1 ( a b ) )
توزیع گاوسی معکوس و توزیع گاما حالت های خاصی از توزیع گاوسی معکوس تعمیم یافته با p = − 1 / 2 و b = 0 هستند. [ ۲]
به طور دقیق ، یک توزیع گاوسی معکوس با فرم
f ( x ; μ , λ ) = 1 / 2 exp − λ ( x − μ ) 2 2 μ 2 x
یک توزیع گاوسی معکوس تعمیم یافته با a = λ / μ 2 ، b = λ و p = − 1 / 2 است.
یک توزیع گاما با فرم
g ( x ; α , β ) = β α 1 Γ ( α ) x α − 1 e − β x
یک توزیع گاوسی معکوس تعمیم یافته با a = 2 β ، b = 0 و p = α است.
یک توزیع گاما معکوس، یک توزیع گاوسی معکوس تعمیم یافته با a = 0 و p < 0 است. [ ۳]
یک توزیع هایپربولیک، یک توزیع گاوسی معکوس تعمیم یافته با p = 0 است. [ ۲]
X و Y را دو متغیر تصادفی مستقل از هم در نظر بگیرید به طوری که X > 0 و Y ∼ γ ( p , a 2 ) برای p , a > 0 . در این صورت داریم X = d 1 Y + X اگر و فقط اگر X ∼ G I G ( − p , a , a ) .
X ، Y 1 و Y 2 را سه متغیر تصادفی مستقل از هم در نظر بگیرید به طوری که X > 0 ، Y 1 ∼ γ ( p , b 2 ) و Y 2 ∼ γ ( p , a 2 ) برای p , a , b > 0 . در این صورت داریم X = d 1 Y 1 + 1 Y 2 + X اگر و فقط اگر X ∼ G I G ( − p , a , b ) .
به طور کلی اگر ( Y i ) i ≥ 1 یک دنباله از متغیر تصادفی های مستقل از هم باشد به طوری که L ( Y 2 i − 1 ) = L ( Y 1 ) = γ ( λ , b 2 ) و L ( Y 2 i ) = L ( Y 2 ) = γ ( λ , a 2 ) برای i ≥ 1 ، آنگاه داریم:

