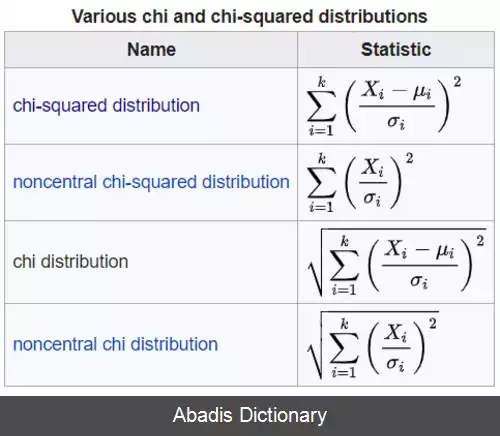
در نظریه امار و احتمال، توزیع احتمال chi یک توزیع پیوسته است. این توزیع برابر ریشه جمع مربعات مجموعه ای از متغییرهای تصادفی است که هر یک به طور مستقل از توزیع نرمال پیروی می کنند.
از توزیع های مشابه chi می توان به توزیع Rayleigh ( توزیع chi با دو درجه آزادی ) و توزیع ماکسول - بولتزمن در توصیف سرعت مولکول ها در گاز ایده آل ( توزیع chi با سه درجع آزادی ) ، اشاره کرد.
اگر Xiهای k متغیر مستقل با توزیع احتمال نرمال باشند ( با میانگین و واریانس ، μ و σ ) حاصل عبارت زیر بیانگر توزیع chi است.
Y = ∑ k = 1 k ( ( X i − μ i ) / σ i ) 2 )
توزیع احتمال chi دارای پارامتری تحت عنوان درجه آزادی ( k ) است، که نمایانگر تعداد - - - - است.
تابع چگالی احتمال ( PDF ) این توزیع به شکل زیر است:
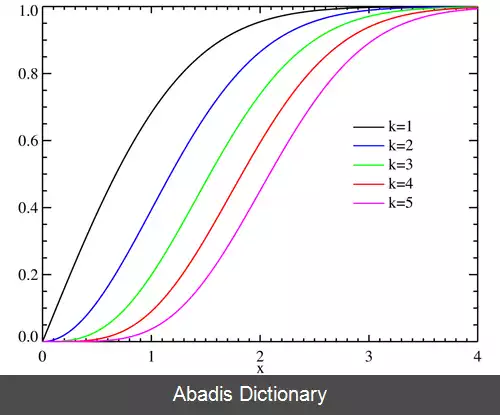
تابع توزیع تجمعی ( CDF ) این توزیع از رابطه زیر قابل محاسبه است:
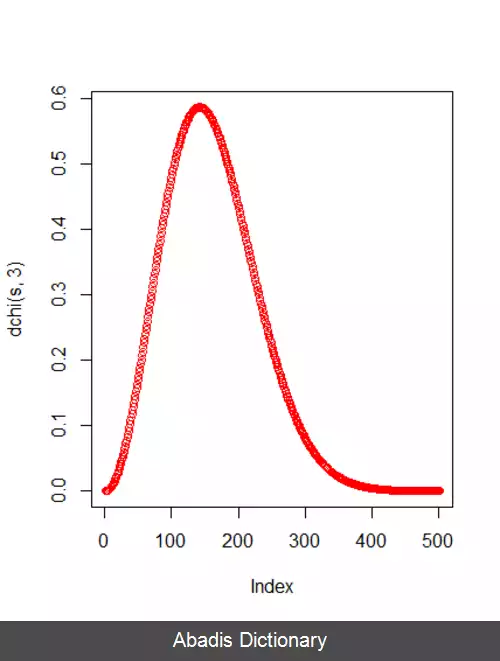
dchi ( x, df, ncp = 0, log = FALSE ) pchi ( q, df, ncp = 0, lower. tail = TRUE, log. p = FALSE ) qchi ( p, df, ncp = 0, lower. tail = TRUE, log. p = FALSE ) rchi ( n, df, ncp = 0 ) x, q vector of quantiles. df degrees of freedom ( non - negative, but can be non - integer ) . ncp non - centrality parameter ( non - negative ) . log, log. p logical; if TRUE, probabilities p are given as log ( p ) . lower. tail logical; if TRUE ( default ) , probabilities are P otherwise, P. p vector of probabilities. n number of observations. If length ( n ) > 1, the length is taken to be the number required. مثال s < - seq ( 0, 5, 0. 1 ) plot ( dchi ( s, 3 ) , type = ‘b’, col = “red” ) قطعه کد بالا نمودار زیر را در plot چاپ می کند.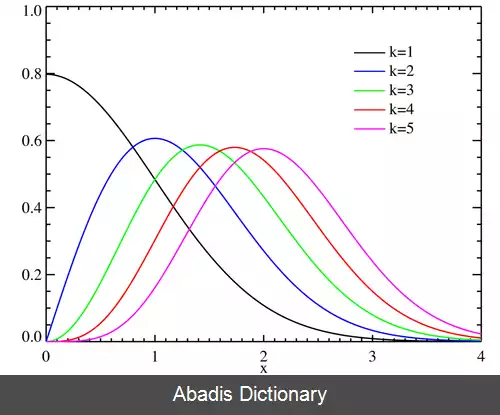
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاز توزیع های مشابه chi می توان به توزیع Rayleigh ( توزیع chi با دو درجه آزادی ) و توزیع ماکسول - بولتزمن در توصیف سرعت مولکول ها در گاز ایده آل ( توزیع chi با سه درجع آزادی ) ، اشاره کرد.
اگر Xiهای k متغیر مستقل با توزیع احتمال نرمال باشند ( با میانگین و واریانس ، μ و σ ) حاصل عبارت زیر بیانگر توزیع chi است.
Y = ∑ k = 1 k ( ( X i − μ i ) / σ i ) 2 )
توزیع احتمال chi دارای پارامتری تحت عنوان درجه آزادی ( k ) است، که نمایانگر تعداد - - - - است.
تابع چگالی احتمال ( PDF ) این توزیع به شکل زیر است:
تابع توزیع تجمعی ( CDF ) این توزیع از رابطه زیر قابل محاسبه است:
dchi ( x, df, ncp = 0, log = FALSE ) pchi ( q, df, ncp = 0, lower. tail = TRUE, log. p = FALSE ) qchi ( p, df, ncp = 0, lower. tail = TRUE, log. p = FALSE ) rchi ( n, df, ncp = 0 ) x, q vector of quantiles. df degrees of freedom ( non - negative, but can be non - integer ) . ncp non - centrality parameter ( non - negative ) . log, log. p logical; if TRUE, probabilities p are given as log ( p ) . lower. tail logical; if TRUE ( default ) , probabilities are P otherwise, P. p vector of probabilities. n number of observations. If length ( n ) > 1, the length is taken to be the number required. مثال s < - seq ( 0, 5, 0. 1 ) plot ( dchi ( s, 3 ) , type = ‘b’, col = “red” ) قطعه کد بالا نمودار زیر را در plot چاپ می کند.




wiki: توزیع کی
