در نظریه آمار و احتمالات، توزیع لِوی یک توزیع احتمالی پیوسته است که برای یک متغیر تصادفی غیر منفی تعریف می شود. در طیف سنجی، این توزیع که در آن فرکانس متغیر وابسته است، با نامِ پروفیل ون در والس شناخته می شود. [ ۱] همچنین این توزیع یک مورد خاص از توزیع گامای وارونه است. توزیع لِوی یک توزیع پایدار است. [ ۲]
تابع چگالی احتمال توزیع لوی در دامنه x ≥ μ برابر است با:
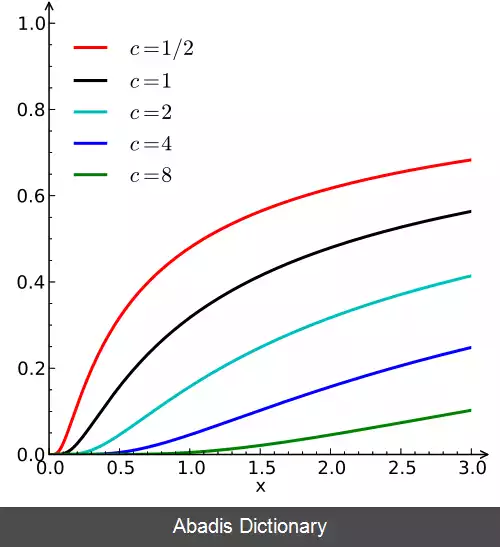
در اینجا μ پارامتر مکان و c پارامتر مقیاس است. تابع توزیع تجمعی توزیع برابر است با:
در اینجا erfc ( z ) تابع خطای مکمل است. پارامتر تغییر مکانِ μ کل منحنی را به سمت راست به اندازه μ منتقل می کند. مانند تمام توزیع های پایدار، توزیع لِوی یک شکل استاندارد دارد که خاصیت پایین را دارا می باشد:
در اینجا y با مقدار پایین برابر است:
تابع مشخصهی توزیع لِوی برابر است با:
این تابع مشخصه همچنین می تواند به همان شکلی که برای توزیع پایدار با α = 1 2 و β = 1 نوشته می شود، نوشته شود.
گشتاور n ام توزیع لِوی با فرض اینکه μ = 0 باشد برابر است با:
تمامی این گشتاورها واگرا هستند. این به این معنی است که این گشتاورها در واقع وجود ندارند. همچنین تابع مولد گشتاورها به این شکل تعریف می شود:
همان طور که معادله خط پیشین نشان می دهد برای تمام t > 0 مقدار انتگرال واگراست و در اطراف صفر تعریف نشده است. از این رو تابع مولد گشتاور نیز تعریف نشده است. مضاف بر این مانند تمام توزیع های پایدار به غیر از توزیع طبیعی، این توزیع دم سنگین و دم کلفت است، یعنی برای x → ∞ تابع f به معادله پایین میل می کند:
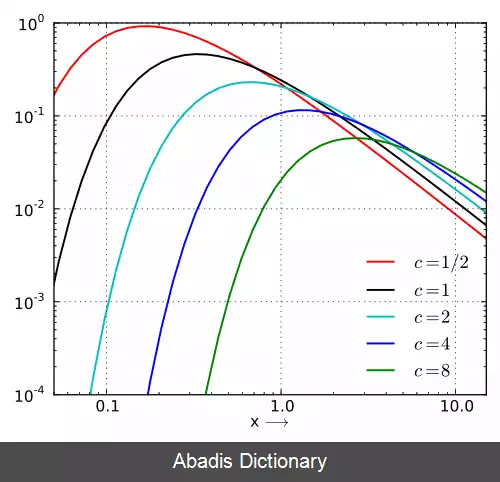
این خصیصه در شکل پایین به خوبی نشان داده شده است. در اینجا μ = 0 و بردارها در مقیاس لگاریتمی رسم شده اند.
توزیع استاندارد لِوی شرایط یک توزیع پایدار را برآورده می کند:[ ۳]
در اینجا X 1 , X 2 , … , X n , X متغیرهای تصادفی مستقلی هستند که همگی از توزیع استاندارد لِوی متابعت می کنند، در اینجا α = 1 / 2 .
• X ∼ Levy ( μ , c ) {\displaystyle X\sim {\textrm {Levy}} ( \mu , c ) \, } اگر آنگاه k X + b ∼ Levy ( k μ + b , k c ) {\displaystyle kX+b\sim {\textrm {Levy}} ( k\mu +b, kc ) \, }
• اگر X ∼ Levy ( 0 , c ) {\displaystyle X\, \sim \, {\textrm {Levy}} ( 0, c ) } آنگاه X ∼ Inv - Gamma ( 1 2 , c 2 ) {\displaystyle X\, \sim \, {\textrm {Inv - Gamma}} ( {\tfrac {1}{2}}, {\tfrac {c}{2}} ) }
• اگر Y ∼ Normal ( μ , σ ) {\displaystyle Y\, \sim \, {\textrm {Normal}} ( \mu , \sigma ) } آنگاه ( Y − μ ) − 2 ∼ Levy ( 0 , 1 / σ 2 ) {\displaystyle { ( Y - \mu ) }^{ - 2}\sim \, {\textrm {Levy}} ( 0, 1/\sigma ^{2} ) }
• اگر X ∼ Normal ( μ , 1 σ ) {\displaystyle X\sim {\textrm {Normal}} ( \mu , {\tfrac {1}{\sqrt {\sigma }}} ) \, } آنگاه ( X − μ ) − 2 ∼ Levy ( 0 , σ ) {\displaystyle { ( X - \mu ) }^{ - 2}\sim {\textrm {Levy}} ( 0, \sigma ) \, }
• اگر X ∼ Levy ( μ , c ) {\displaystyle X\, \sim \, {\textrm {Levy}} ( \mu , c ) } آنگاه X ∼ Stable ( 1 / 2 , 1 , c , μ ) {\displaystyle X\, \sim \, {\textrm {Stable}} ( 1/2, 1, c, \mu ) \, }
• اگر X ∼ Levy ( 0 , c ) {\displaystyle X\, \sim \, {\textrm {Levy}} ( 0, c ) } آنگاه X ∼ Scale - inv - χ 2 ( 1 , c ) {\displaystyle X\, \sim \, {\textrm {Scale - inv - }}\chi ^{2} ( 1, c ) }
• اگر X ∼ Levy ( μ , c ) {\displaystyle X\, \sim \, {\textrm {Levy}} ( \mu , c ) } آنگاه ( X − μ ) − 1 2 ∼ FoldedNormal ( 0 , 1 / c ) {\displaystyle { ( X - \mu ) }^{ - {\tfrac {1}{2}}}\sim \, {\textrm {FoldedNormal}} ( 0, 1/{\sqrt {c}} ) }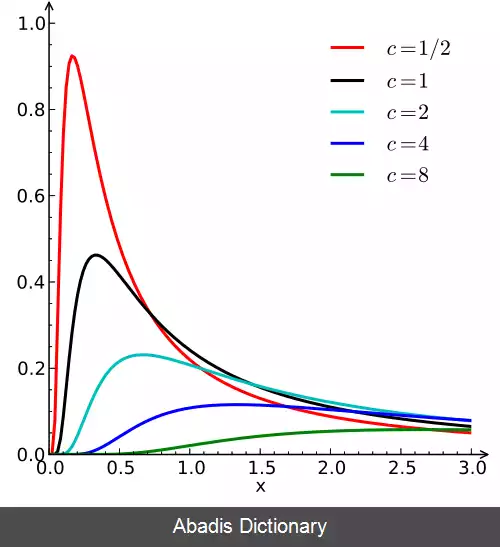
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتابع چگالی احتمال توزیع لوی در دامنه x ≥ μ برابر است با:
در اینجا μ پارامتر مکان و c پارامتر مقیاس است. تابع توزیع تجمعی توزیع برابر است با:
در اینجا erfc ( z ) تابع خطای مکمل است. پارامتر تغییر مکانِ μ کل منحنی را به سمت راست به اندازه μ منتقل می کند. مانند تمام توزیع های پایدار، توزیع لِوی یک شکل استاندارد دارد که خاصیت پایین را دارا می باشد:
در اینجا y با مقدار پایین برابر است:
تابع مشخصهی توزیع لِوی برابر است با:
این تابع مشخصه همچنین می تواند به همان شکلی که برای توزیع پایدار با α = 1 2 و β = 1 نوشته می شود، نوشته شود.
گشتاور n ام توزیع لِوی با فرض اینکه μ = 0 باشد برابر است با:
تمامی این گشتاورها واگرا هستند. این به این معنی است که این گشتاورها در واقع وجود ندارند. همچنین تابع مولد گشتاورها به این شکل تعریف می شود:
همان طور که معادله خط پیشین نشان می دهد برای تمام t > 0 مقدار انتگرال واگراست و در اطراف صفر تعریف نشده است. از این رو تابع مولد گشتاور نیز تعریف نشده است. مضاف بر این مانند تمام توزیع های پایدار به غیر از توزیع طبیعی، این توزیع دم سنگین و دم کلفت است، یعنی برای x → ∞ تابع f به معادله پایین میل می کند:
این خصیصه در شکل پایین به خوبی نشان داده شده است. در اینجا μ = 0 و بردارها در مقیاس لگاریتمی رسم شده اند.
توزیع استاندارد لِوی شرایط یک توزیع پایدار را برآورده می کند:[ ۳]
در اینجا X 1 , X 2 , … , X n , X متغیرهای تصادفی مستقلی هستند که همگی از توزیع استاندارد لِوی متابعت می کنند، در اینجا α = 1 / 2 .
• X ∼ Levy ( μ , c ) {\displaystyle X\sim {\textrm {Levy}} ( \mu , c ) \, } اگر آنگاه k X + b ∼ Levy ( k μ + b , k c ) {\displaystyle kX+b\sim {\textrm {Levy}} ( k\mu +b, kc ) \, }
• اگر X ∼ Levy ( 0 , c ) {\displaystyle X\, \sim \, {\textrm {Levy}} ( 0, c ) } آنگاه X ∼ Inv - Gamma ( 1 2 , c 2 ) {\displaystyle X\, \sim \, {\textrm {Inv - Gamma}} ( {\tfrac {1}{2}}, {\tfrac {c}{2}} ) }
• اگر Y ∼ Normal ( μ , σ ) {\displaystyle Y\, \sim \, {\textrm {Normal}} ( \mu , \sigma ) } آنگاه ( Y − μ ) − 2 ∼ Levy ( 0 , 1 / σ 2 ) {\displaystyle { ( Y - \mu ) }^{ - 2}\sim \, {\textrm {Levy}} ( 0, 1/\sigma ^{2} ) }
• اگر X ∼ Normal ( μ , 1 σ ) {\displaystyle X\sim {\textrm {Normal}} ( \mu , {\tfrac {1}{\sqrt {\sigma }}} ) \, } آنگاه ( X − μ ) − 2 ∼ Levy ( 0 , σ ) {\displaystyle { ( X - \mu ) }^{ - 2}\sim {\textrm {Levy}} ( 0, \sigma ) \, }
• اگر X ∼ Levy ( μ , c ) {\displaystyle X\, \sim \, {\textrm {Levy}} ( \mu , c ) } آنگاه X ∼ Stable ( 1 / 2 , 1 , c , μ ) {\displaystyle X\, \sim \, {\textrm {Stable}} ( 1/2, 1, c, \mu ) \, }
• اگر X ∼ Levy ( 0 , c ) {\displaystyle X\, \sim \, {\textrm {Levy}} ( 0, c ) } آنگاه X ∼ Scale - inv - χ 2 ( 1 , c ) {\displaystyle X\, \sim \, {\textrm {Scale - inv - }}\chi ^{2} ( 1, c ) }
• اگر X ∼ Levy ( μ , c ) {\displaystyle X\, \sim \, {\textrm {Levy}} ( \mu , c ) } آنگاه ( X − μ ) − 1 2 ∼ FoldedNormal ( 0 , 1 / c ) {\displaystyle { ( X - \mu ) }^{ - {\tfrac {1}{2}}}\sim \, {\textrm {FoldedNormal}} ( 0, 1/{\sqrt {c}} ) }



wiki: توزیع لوی
