توزیع لاگ - نرمال ( به انگلیسی: log - normal یا lognormal ) در نظریه احتمال نوعی توزیع احتمال پیوسته برای یک متغیر تصادفی است، که لگاریتم آن به صورت نرمال توزیع شده است.
از این رو اگر متغیر تصادفی X به صورت لاگ - نرمال توزیع شده باشد، آنوقت Y = ln ( X ) دارای توزیع نرمال است. [ ۱] [ ۲] [ ۳] به بیان دیگر، اگر Yدارای توزیع نرمال باشد، آنوقت تابع نمایی Y، یعنی X = exp ( Y ) دارای توزیع لاگ - نرمال است. متغیر تصادفی که به صورت لاگ - نرمال توزیع شده است، فقط مقادیر مثبت و حقیقی را می پذیرد.
توزیع لاگ - نرمال مدلی مفید و مناسب برای اندازه گیری ها در علوم دقیق و مهندسی، مثل پزشکی، اقتصاد و دیگر عناوین است ( مثلا انرژی، غلظت، طول، بازدهی مالی، و دیگر سنجه ها ) .
به این توزیع، بعضی مواقع توزیع گالتون ( به انگلیسی: Galton distribution ) هم می گویند که به افتخار فرانسیس گالتون نامگذاری شده است. [ ۴] توزیع لاگ - نرمال با دیگر اسامی مثل مک آلیستر ( به انگلیسی: McAlister ) , جبرات ( به انگلیسی: Gibrat ) و کاب – داگلاس ( به انگلیسی: Cobb–Douglas ) نیز مرتبط است. [ ۴]
یک فرایند لاگ - نرمال، یک فهم آماری از حاصل ضرب چندین متغیر تصادفی مستقل است، که همه آن ها مثبت هستند. این موضوع از طریق درنظرگرفتن قضیه حد مرکزی در دامنه لاگ قابل توجیه است. توزیع لاگ - نرمال همان توزیع احتمال با آنتروپی حداکثری برای متغیر تصادفی X است که در آن میانگین و واریانس ln ( X ) از قبل معین بوده است. [ ۵]
فرض کنید که Z یک متغیر تصادفی با توزیع نرمال استاندارد باشد، و همچنین فرض کنید که μ و σ > 0 دو عدد حقیقی باشند. آنوقت توزیع متغیر تصادفی
X = e μ + σ Z
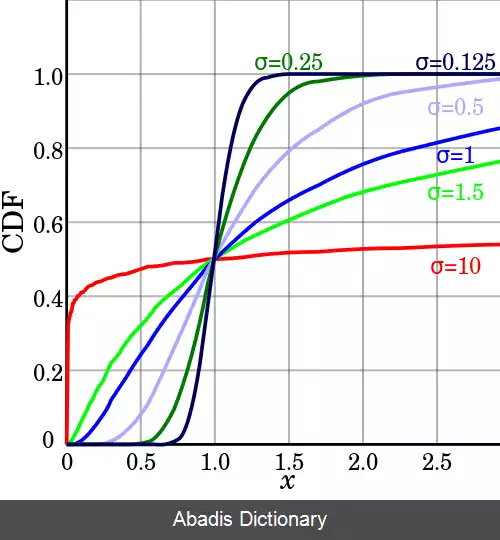
یک توزیع لاگ - نرمال با پارامترهای μ و σ نامیده می شود. این پارامترها مقدار چشمداشتی ( یا میانگین ) و انحراف معیار برای لگاریتم طبیعی متغیر X هستند، و نه خود X .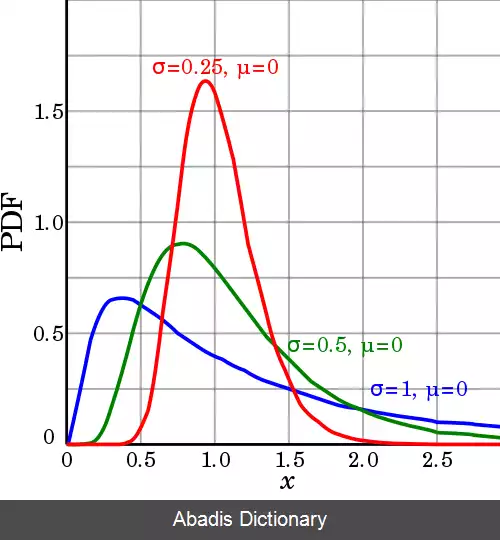
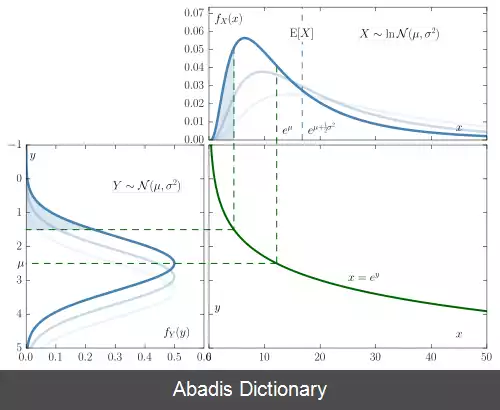
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاز این رو اگر متغیر تصادفی X به صورت لاگ - نرمال توزیع شده باشد، آنوقت Y = ln ( X ) دارای توزیع نرمال است. [ ۱] [ ۲] [ ۳] به بیان دیگر، اگر Yدارای توزیع نرمال باشد، آنوقت تابع نمایی Y، یعنی X = exp ( Y ) دارای توزیع لاگ - نرمال است. متغیر تصادفی که به صورت لاگ - نرمال توزیع شده است، فقط مقادیر مثبت و حقیقی را می پذیرد.
توزیع لاگ - نرمال مدلی مفید و مناسب برای اندازه گیری ها در علوم دقیق و مهندسی، مثل پزشکی، اقتصاد و دیگر عناوین است ( مثلا انرژی، غلظت، طول، بازدهی مالی، و دیگر سنجه ها ) .
به این توزیع، بعضی مواقع توزیع گالتون ( به انگلیسی: Galton distribution ) هم می گویند که به افتخار فرانسیس گالتون نامگذاری شده است. [ ۴] توزیع لاگ - نرمال با دیگر اسامی مثل مک آلیستر ( به انگلیسی: McAlister ) , جبرات ( به انگلیسی: Gibrat ) و کاب – داگلاس ( به انگلیسی: Cobb–Douglas ) نیز مرتبط است. [ ۴]
یک فرایند لاگ - نرمال، یک فهم آماری از حاصل ضرب چندین متغیر تصادفی مستقل است، که همه آن ها مثبت هستند. این موضوع از طریق درنظرگرفتن قضیه حد مرکزی در دامنه لاگ قابل توجیه است. توزیع لاگ - نرمال همان توزیع احتمال با آنتروپی حداکثری برای متغیر تصادفی X است که در آن میانگین و واریانس ln ( X ) از قبل معین بوده است. [ ۵]
فرض کنید که Z یک متغیر تصادفی با توزیع نرمال استاندارد باشد، و همچنین فرض کنید که μ و σ > 0 دو عدد حقیقی باشند. آنوقت توزیع متغیر تصادفی
X = e μ + σ Z
یک توزیع لاگ - نرمال با پارامترهای μ و σ نامیده می شود. این پارامترها مقدار چشمداشتی ( یا میانگین ) و انحراف معیار برای لگاریتم طبیعی متغیر X هستند، و نه خود X .



wiki: توزیع لاگ نرمال
