در نظریه آمار و احتمالات، توزیع لاپلاس ( laplace distribution ) ، توزیعی پیوسته است که بنام پیِر سیمون دو لاپلاس ( Pierre - Simon de Laplace ) نامگذاری شده. گاهی نیز توزیع نمایی دوتایی نامیده می شود، چراکه همانند دو توزیع نمایی که کنار همدیگر قرار داده شده اند، می ماند. جالب است بدانید این نام برخی اوقات برای خطاب توزیع گامبل نیز مورد استفاده قرار می گیرد.
این توزیع به بیان ساده، نمایانگر تفاوت دو متغیر تصادفی مستقل که از توزیع نمایی پیروی می کنند، می باشد.
کاربرد معمول این توزیع، برای مدل کردن نمونه هایی است که آرام تر از توزیع نمایی به صفر میل می کنند ( یا به عبارت آماری از توزیع دم سنگین پیروی می کنند ) .
به طور مثال افزایش جنبش لاپلاس یا پراکندگی عملیات گاما که در یک مقیاس زمانی اندازه گیری می شود، از توزیع لاپلاس پیروی می کنند.
تابع چگالی احتمال توزیع لاپلاس با پارامترهای μ و b:
= 1 2 b { exp ( − μ − x b ) if x < μ exp ( − x − μ b ) if x ≥ μ f ( x ∣ μ , b ) = 1 2 b exp ( − | x − μ | b )
در اینجا، μ یک پارامتر مکانی است و b> ۰، که برخی اوقات به عنوان انحراف بیان می شود، یک پارامتر مقیاس است. اگر μ = 0 و b = 1 ، نیم خط مثبت دقیقاً یک توزیع نمایی با مقیاس ۱/۲ خواهد بود.
تابع چگالی احتمال لاپلاس همچنین یادآور توزیع نرمال است؛ گرچه، برخلاف توزیع نرمال که براساس مجذور اختلاف با میانگین ( μ ) بیان می شود، چگالی لاپلاس براساس قدر مطلق تفاضل از میانگین بیان می گردد. در نتیجه، توزیع لاپلاس دنباله بزرگتری از توزیع نرمال دارد.
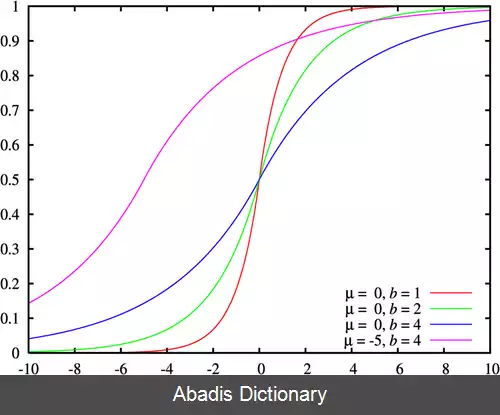
توزیع لاپلاس برای انتگرال گیری راحت است ( با توجه به تقارن توزیع ) بخاطر وجود تابع قدرمطلق. تابع توزیع تجمعی آن به صورت زیر است:
F ( x ) = ∫ − ∞ x f ( u ) d u = { 1 2 exp ( x − μ b ) if x < μ 1 − 1 2 exp ( − x − μ b ) if x ≥ μ = 1 2 + 1 2 sgn ( x − μ ) ( 1 − exp ( − | x − μ | b ) ) .
تابع وارون تجمعی آن همانند زیر است: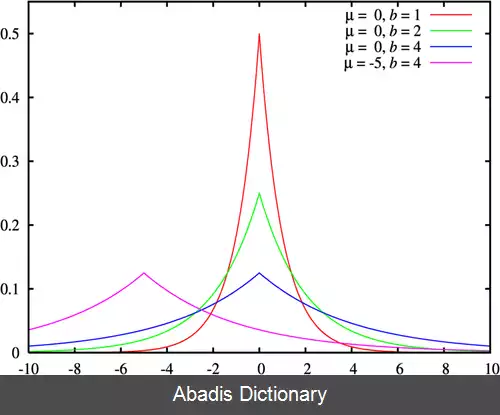
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین توزیع به بیان ساده، نمایانگر تفاوت دو متغیر تصادفی مستقل که از توزیع نمایی پیروی می کنند، می باشد.
کاربرد معمول این توزیع، برای مدل کردن نمونه هایی است که آرام تر از توزیع نمایی به صفر میل می کنند ( یا به عبارت آماری از توزیع دم سنگین پیروی می کنند ) .
به طور مثال افزایش جنبش لاپلاس یا پراکندگی عملیات گاما که در یک مقیاس زمانی اندازه گیری می شود، از توزیع لاپلاس پیروی می کنند.
تابع چگالی احتمال توزیع لاپلاس با پارامترهای μ و b:
= 1 2 b { exp ( − μ − x b ) if x < μ exp ( − x − μ b ) if x ≥ μ f ( x ∣ μ , b ) = 1 2 b exp ( − | x − μ | b )
در اینجا، μ یک پارامتر مکانی است و b> ۰، که برخی اوقات به عنوان انحراف بیان می شود، یک پارامتر مقیاس است. اگر μ = 0 و b = 1 ، نیم خط مثبت دقیقاً یک توزیع نمایی با مقیاس ۱/۲ خواهد بود.
تابع چگالی احتمال لاپلاس همچنین یادآور توزیع نرمال است؛ گرچه، برخلاف توزیع نرمال که براساس مجذور اختلاف با میانگین ( μ ) بیان می شود، چگالی لاپلاس براساس قدر مطلق تفاضل از میانگین بیان می گردد. در نتیجه، توزیع لاپلاس دنباله بزرگتری از توزیع نرمال دارد.
توزیع لاپلاس برای انتگرال گیری راحت است ( با توجه به تقارن توزیع ) بخاطر وجود تابع قدرمطلق. تابع توزیع تجمعی آن به صورت زیر است:
F ( x ) = ∫ − ∞ x f ( u ) d u = { 1 2 exp ( x − μ b ) if x < μ 1 − 1 2 exp ( − x − μ b ) if x ≥ μ = 1 2 + 1 2 sgn ( x − μ ) ( 1 − exp ( − | x − μ | b ) ) .
تابع وارون تجمعی آن همانند زیر است:




wiki: توزیع لاپلاس
