توزیع دوجمله ای
فرهنگستان زبان و ادب
دانشنامه عمومی
توزیع دوجمله ای[ ۱] نوعی توزیع پرکاربرد در آمار، اقتصاد، و علوم تجربی است. در نظریهٔ احتمال و آمار توزیع دوجمله ای توزیعی گسسته است از تعداد موفقیت ها در دنباله ای شامل n آزمایش مستقل برنولی همه با احتمال موفقیت p ( توزیع برنولی ) . در واقع متغیر تصادفی X ( تعداد موفقیت ها ) را متغیر دوجمله ای با پارامترهای n و p می گویند.
یک آزمایش دوجمله ای بایستی دارای ویژگی های زیر باشد:[ ۲]
• آزمایش دارای n تعداد آزمون یکسان و عیناً مشابه باشد.
• نتیجه هر آزمون فقط به یکی از این دو صورت باشد: موفق یا ناموفق.
• احتمال موفقیت آزمونی را اگر با p نشان دهیم، از آزمون به آزمون یکسان بوده و متغیر نباشد. احتمال ناموفقیت را با q نشان داده که برابر است با q=1 - p
• آزمون ها مستقل باشند.
درحالت کلی اگر X یک متغیر تصادفی دوجمله ای با پارامترهای p, n باشد، آن را به صورت ( X ~ B ( n, p نمایش می دهیم. احتمال بدست آوردن k موفقیت با تابع جرم احتمال زیر مشخص می شود:
حال می خواهیم بررسی کنیم که این فرمول چگونه بدست آمده است: توجه کنید که تعداد راه های ممکن در انجام n آزمایش برنولی که می تواند به k موفقیت منتهی شود برابر است با تعداد دنباله های مختلف به طول n از حروف b , a با k حرف a ( موفقیت ) و n - k حرف b ( شکست ) . اما تعداد این دنباله ها برابر است با ( n k ) ، زیرا تعداد جایگشت های متمایز n حرف از دو نوع مختلف، که k تا همانند از نوع اول و n - k تا همانند از نوع دوم وجود دارد برابر است با n ! k ! ( n − k ) ! . باتوجه به استقلال امتحان ها چون احتمال هریک از این دنباله پیشامدها برابر p k ( 1 − p ) n − k است داریم:
دلیل اینکه به این توزیع دوجمله ای می گویند این است که قضیهٔ بسط دوجمله ای تضمین می کند که p ( k ) یک تابع جرم احتمال است:
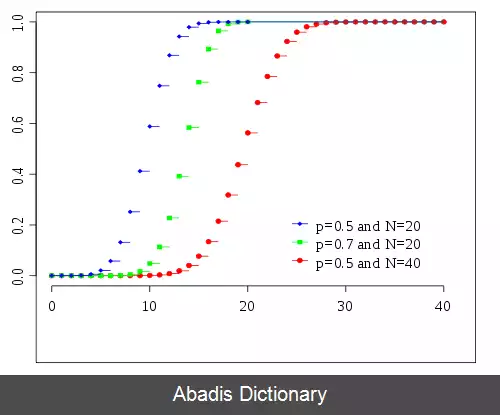
تابع توزیع تجمعی متغیر تصادفی دوجمله ای به شکل زیر است:
اگر یک تیرانداز با احتمال ۰/۷ تیری را به هدف بزند و x تعداد تیرهای به هدف خورده در ۵ شلیک باشد؛ ابتدا توزیع احتمال x را معلوم کنید و هر یک از احتمال های زیر را به دست آورید. الف - دقیقاً ۳ تیر به هدف بزند. ب - حداکثر ۲ تیر به هدف بزند. ج - هیچ تیری به هدف نزند. متغیر تصادفی x، دارای توزیع دو جمله ای با پارامترهای n=۵ , p=۰٫۷ است که تابع احتمال آن را به صورت زیر می نویسیم: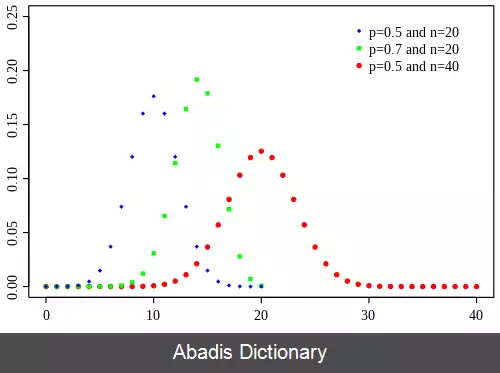
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک آزمایش دوجمله ای بایستی دارای ویژگی های زیر باشد:[ ۲]
• آزمایش دارای n تعداد آزمون یکسان و عیناً مشابه باشد.
• نتیجه هر آزمون فقط به یکی از این دو صورت باشد: موفق یا ناموفق.
• احتمال موفقیت آزمونی را اگر با p نشان دهیم، از آزمون به آزمون یکسان بوده و متغیر نباشد. احتمال ناموفقیت را با q نشان داده که برابر است با q=1 - p
• آزمون ها مستقل باشند.
درحالت کلی اگر X یک متغیر تصادفی دوجمله ای با پارامترهای p, n باشد، آن را به صورت ( X ~ B ( n, p نمایش می دهیم. احتمال بدست آوردن k موفقیت با تابع جرم احتمال زیر مشخص می شود:
حال می خواهیم بررسی کنیم که این فرمول چگونه بدست آمده است: توجه کنید که تعداد راه های ممکن در انجام n آزمایش برنولی که می تواند به k موفقیت منتهی شود برابر است با تعداد دنباله های مختلف به طول n از حروف b , a با k حرف a ( موفقیت ) و n - k حرف b ( شکست ) . اما تعداد این دنباله ها برابر است با ( n k ) ، زیرا تعداد جایگشت های متمایز n حرف از دو نوع مختلف، که k تا همانند از نوع اول و n - k تا همانند از نوع دوم وجود دارد برابر است با n ! k ! ( n − k ) ! . باتوجه به استقلال امتحان ها چون احتمال هریک از این دنباله پیشامدها برابر p k ( 1 − p ) n − k است داریم:
دلیل اینکه به این توزیع دوجمله ای می گویند این است که قضیهٔ بسط دوجمله ای تضمین می کند که p ( k ) یک تابع جرم احتمال است:
تابع توزیع تجمعی متغیر تصادفی دوجمله ای به شکل زیر است:
اگر یک تیرانداز با احتمال ۰/۷ تیری را به هدف بزند و x تعداد تیرهای به هدف خورده در ۵ شلیک باشد؛ ابتدا توزیع احتمال x را معلوم کنید و هر یک از احتمال های زیر را به دست آورید. الف - دقیقاً ۳ تیر به هدف بزند. ب - حداکثر ۲ تیر به هدف بزند. ج - هیچ تیری به هدف نزند. متغیر تصادفی x، دارای توزیع دو جمله ای با پارامترهای n=۵ , p=۰٫۷ است که تابع احتمال آن را به صورت زیر می نویسیم:
wiki: توزیع دوجمله ای
پیشنهاد کاربران
پیشنهادی ثبت نشده است. شما اولین نفر باشید