توزیع تعمیم یافته گاما یک توزیع احتمال پیوسته است که با سه پارامتر تعریف می شود. این توزیع در حقیقت یک تعمیم از توزیع گامای دو پارامتره است. از آنجا که بسیاری از توزیعهایی که برای آنالیز بقا مورد استفاده قرار می گیرند ( مانند توزیع نمایی، توزیع وایبول، توزیع گاما و توزیع نیمه نرمال ) موارد خاصی از توزیع تمیم یافته گاما هستند، گاهی اوقات از این توزیع برای تعیین مدل مناسب با توجه به مجموعه داده ها استفاده می کنند. [ ۱]
توزیع تعمیم یافته گاما دارای سه پارامتر است: a > 0 ، d > 0 ، و p > 0 . برای x غیر منفی، تابع چگالی احتمال گامای تعمیم یافته عبارت است از:[ ۲]
f ( x ; a , d , p ) = ( p / a d ) x d − 1 e − ( x / a ) p Γ ( d / p )
در اینجا Γ ( ⋅ ) تابع گاما را نشان می دهد.
تابع توزیع تجمعی برابر است با:
F ( x ; a , d , p ) = γ ( d / p , ( x / a ) p ) Γ ( d / p )
در اینجا γ ( ⋅ ) تابع گاما ناقص پایین را نشان می دهد.
اگر d = p آنگاه توزیع تعمیم یافته گاما به توزیع وایبول تبدیل می شود. همچنین اگر p = 1 آنگاه توزیع تعمیم یافته گام به توزیع گاما تبدیل می شود.
اگر X یک توزیع تعمیم یافته گاما باشد گشتاورهای آن عبارت خواهند بود از:[ ۳]
E ( X r ) = a r Γ ( d + r p ) Γ ( d p )
اگر f 1 و f 2 توابع چگالی احتمال دو توزیع تعمیم یافته گاما باشند، آنگاه معیار واگرایی کولبک - لایبلر آنها برابر خواهد بود با:
D K L ( f 1 ∥ f 2 ) = ∫ 0 ∞ f 1 ( x ; a 1 , d 1 , p 1 ) ln f 1 ( x ; a 1 , d 1 , p 1 ) f 2 ( x ; a 2 , d 2 , p 2 ) d x = ln p 1 a 2 d 2 Γ ( d 2 / p 2 ) p 2 a 1 d 1 Γ ( d 1 / p 1 ) + ( d 1 − d 2 ) + Γ ( ( d 1 + p 2 ) / p 1 ) Γ ( d 1 / p 1 ) ( a 1 a 2 ) p 2 − d 1 p 1
در اینجا ψ ( ⋅ ) تابع دایگما است. [ ۴]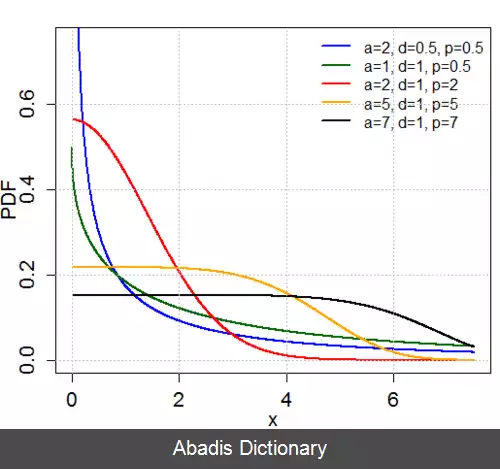
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتوزیع تعمیم یافته گاما دارای سه پارامتر است: a > 0 ، d > 0 ، و p > 0 . برای x غیر منفی، تابع چگالی احتمال گامای تعمیم یافته عبارت است از:[ ۲]
f ( x ; a , d , p ) = ( p / a d ) x d − 1 e − ( x / a ) p Γ ( d / p )
در اینجا Γ ( ⋅ ) تابع گاما را نشان می دهد.
تابع توزیع تجمعی برابر است با:
F ( x ; a , d , p ) = γ ( d / p , ( x / a ) p ) Γ ( d / p )
در اینجا γ ( ⋅ ) تابع گاما ناقص پایین را نشان می دهد.
اگر d = p آنگاه توزیع تعمیم یافته گاما به توزیع وایبول تبدیل می شود. همچنین اگر p = 1 آنگاه توزیع تعمیم یافته گام به توزیع گاما تبدیل می شود.
اگر X یک توزیع تعمیم یافته گاما باشد گشتاورهای آن عبارت خواهند بود از:[ ۳]
E ( X r ) = a r Γ ( d + r p ) Γ ( d p )
اگر f 1 و f 2 توابع چگالی احتمال دو توزیع تعمیم یافته گاما باشند، آنگاه معیار واگرایی کولبک - لایبلر آنها برابر خواهد بود با:
D K L ( f 1 ∥ f 2 ) = ∫ 0 ∞ f 1 ( x ; a 1 , d 1 , p 1 ) ln f 1 ( x ; a 1 , d 1 , p 1 ) f 2 ( x ; a 2 , d 2 , p 2 ) d x = ln p 1 a 2 d 2 Γ ( d 2 / p 2 ) p 2 a 1 d 1 Γ ( d 1 / p 1 ) + ( d 1 − d 2 ) + Γ ( ( d 1 + p 2 ) / p 1 ) Γ ( d 1 / p 1 ) ( a 1 a 2 ) p 2 − d 1 p 1
در اینجا ψ ( ⋅ ) تابع دایگما است. [ ۴]

wiki: توزیع تعمیم یافته گاما
