توزیع برنولی پیوسته[ ۱] [ ۲] [ ۳] در نظریه احتمالات، آمار و یادگیری ماشین، خانواده ای از توزیع های احتمال پیوسته است که توسط پارامتر λ ∈ ( 0 , 1 ) تعریف می شود. بازه این توزیع است و به این شکل تعریف می شود:
توزیع پیوسته برنولی در یادگیری عمیق و بینایی رایانه ای، به ویژه در زمینه رمزگذارهای خودکار متغیر[ ۴] [ ۵] برای مدل سازی پیکسل های تصاویر طبیعی مورد استفاده قرار می گیرد. به این ترتیب، یک همتای احتمالی مناسب برای از دست دادن آنتروپی متقاطع باینری که معمولاً مورد استفاده قرار می گیرد، تعریف می کند که اغلب برای پیوسته اعمال می شود. داده های با ارزش[ ۶] [ ۷] [ ۸] [ ۹] این عمل به معنای نادیده گرفتن ثابت نرمال کننده توزیع پیوسته برنولی است، زیرا از دست دادن آنتروپی متقاطع باینری تنها یک احتمال لگ واقعی را برای گسسته تعریف می کند. { 0 , 1 } داده های با ارزش
برنولی پیوسته نیز یک خانواده نمایی از توزیع ها را تعریف می کند. نوشتن η = log ( λ / ( 1 − λ ) ) برای پارامتر طبیعی، چگالی را می توان به شکل متعارف بازنویسی کرد: p ( x | η ) ∝ exp ( η x ) .
برنولی پیوسته را می توان به عنوان نسخه پیوسته توزیع برنولی در نظر گرفت که بر روی مجموعه گسسته { 0 , 1 } و به وسیله تابع چگالی احتمال پایین تعریف می شود:
جایی که p یک پارامتر عددی بین ۰ و ۱ است. اعمال همین تابع در بازه پیوسته منجر به ضریبی از تابع چگالی احتمال پیوسته برنولی می شود.
توزیع بتا تابع چگالی را پایین را دارد:
که می توان آن را به این شکل نوشت:
در اینجا α 1 , α 2 پارامترهای عددی مثبت هستند و ( x 1 , x 2 ) نشان دهنده یک نقطه دلخواه در داخل سادک Δ 1 = { ( x 1 , x 2 ) : x 1 > 0 , x 2 > 0 , x 1 + x 2 = 1 } می باشد. با تعویض نقش پارامتر و ورودی در این تابع چگالی، عبارت پایین را به دست می آوریم:
با اعمال محدودیت α 1 + α 2 = 1 و تغییر متغیر λ = α 1 به عبارت پایین خواهیم رسید:
که دقیقاً مطابق با چگالی برنولی پیوسته است.
توزیع نمایی محدود به بازه ۰ تا ۱ معادل توزیع برنولی پیوسته با پارامتر مناسب است.
تعمیم چند متغیره برنولی پیوسته، پیوسته - دسته ای نامیده می شود. [ ۱۰]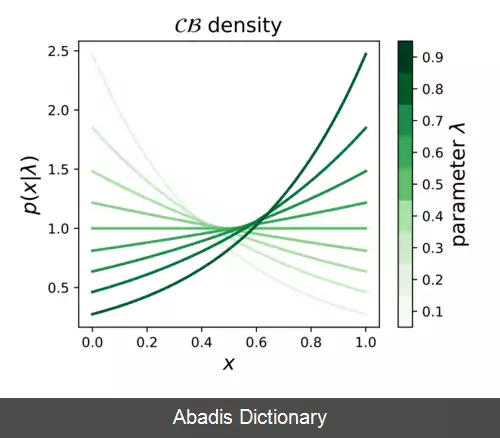
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتوزیع پیوسته برنولی در یادگیری عمیق و بینایی رایانه ای، به ویژه در زمینه رمزگذارهای خودکار متغیر[ ۴] [ ۵] برای مدل سازی پیکسل های تصاویر طبیعی مورد استفاده قرار می گیرد. به این ترتیب، یک همتای احتمالی مناسب برای از دست دادن آنتروپی متقاطع باینری که معمولاً مورد استفاده قرار می گیرد، تعریف می کند که اغلب برای پیوسته اعمال می شود. داده های با ارزش[ ۶] [ ۷] [ ۸] [ ۹] این عمل به معنای نادیده گرفتن ثابت نرمال کننده توزیع پیوسته برنولی است، زیرا از دست دادن آنتروپی متقاطع باینری تنها یک احتمال لگ واقعی را برای گسسته تعریف می کند. { 0 , 1 } داده های با ارزش
برنولی پیوسته نیز یک خانواده نمایی از توزیع ها را تعریف می کند. نوشتن η = log ( λ / ( 1 − λ ) ) برای پارامتر طبیعی، چگالی را می توان به شکل متعارف بازنویسی کرد: p ( x | η ) ∝ exp ( η x ) .
برنولی پیوسته را می توان به عنوان نسخه پیوسته توزیع برنولی در نظر گرفت که بر روی مجموعه گسسته { 0 , 1 } و به وسیله تابع چگالی احتمال پایین تعریف می شود:
جایی که p یک پارامتر عددی بین ۰ و ۱ است. اعمال همین تابع در بازه پیوسته منجر به ضریبی از تابع چگالی احتمال پیوسته برنولی می شود.
توزیع بتا تابع چگالی را پایین را دارد:
که می توان آن را به این شکل نوشت:
در اینجا α 1 , α 2 پارامترهای عددی مثبت هستند و ( x 1 , x 2 ) نشان دهنده یک نقطه دلخواه در داخل سادک Δ 1 = { ( x 1 , x 2 ) : x 1 > 0 , x 2 > 0 , x 1 + x 2 = 1 } می باشد. با تعویض نقش پارامتر و ورودی در این تابع چگالی، عبارت پایین را به دست می آوریم:
با اعمال محدودیت α 1 + α 2 = 1 و تغییر متغیر λ = α 1 به عبارت پایین خواهیم رسید:
که دقیقاً مطابق با چگالی برنولی پیوسته است.
توزیع نمایی محدود به بازه ۰ تا ۱ معادل توزیع برنولی پیوسته با پارامتر مناسب است.
تعمیم چند متغیره برنولی پیوسته، پیوسته - دسته ای نامیده می شود. [ ۱۰]

wiki: توزیع برنولی پیوسته
