توزیع بتا، توزیع احتمال پیوسته ای است که بر بازه تعریف می گردد و به توزیع گاما مرتبط می باشد. توزیع بتا دارای دو پارامتر آزاد است که این دو پارامتر شامل α و β می شوند. تابع چگالی احتمال این توزیع در زیر آورده شده است.
f ( x ) = x α − 1 ( 1 + x ) − α − β B ( α , β )
توزیع بتا نقش مهمی در تئوری آماره ترتیبی دارد. نتیجه بدین گونه است که توزیع kمین کوچک ترین مقدار از یک فضای نمونه nتایی از یک توزیع یکنواخت پیوسته معادل با یک توزیع بتا می باشد. نتیجه به صورت زیر خلاصه می گردد.
U ( k ) ∼ B e t a ( k , n + 1 − k )
موجک یک نوسان موج مانند با دامنه ای است که از صفر شروع می گردد، افزایش می یابد و سپس به صفر تقلیل می یابد. به طور معمول موجک ها را می توان به عنوان نوسان مختصری که به سرعت در حال فروپاشی هستند تجسم کرد. موجک ها می توانند برای استخراج اطلاعات از انواع مختلف داده استفاده گردند. از جمله این داده ها می توان به سیگنال ها و تصاویر صوتی اشاره نمود. به این ترتیب، موجک ها با این هدف ساخته می شوند تا ویژگی های خاصی داشته باشند که آن ها را قادر به پردازش سیگنال سازد. نکته ای که موجک ها را برجسته می سازد این است که آن ها هم در زمان و هم در فرکانس موضعی می باشند در حالی که تبدیل استاندارد فوریه تنها در فرکانس موضعی است. بنابراین، تبدیل استاندارد فوریه فقط برای فرایندهای ثابت قابل استفاده است در حالی که موجک ها برای فرآیندهای غیرثابت نیز قابل استفاده می باشند. موجک ها را می توان بر اساس توزیع بتا ساخت. موجک ساخته شده توسط توزیع بتا را می توان به عنوان یک طیف نرم از موج های هار مشاهده کرد که شکل آن با دو پارامتر α و β مشخص می گردد. [ ۱]
یکی از مهم ترین کاربردهای توزیع بتا استفاده از آن در آنالیز آماری بیزی توزیع دوجمله ای است. درواقع توزیع بتا به عنوان یک مدل برای احتمال موفقیت یک توزیع دوجمله ای استفاده می گردد، به این صورت که توزیع بتا به عنوان یک توزیع پیشین یا پسین برای آنالیز مورد استفاده قرار می گیرد. [ ۲]
f ( x ; α , β ) = x α − 1 ( 1 − x ) β − 1 ∫ 0 3 u α − 1 ( 1 − u ) β − 1 d u
= Γ ( α + β ) Γ ( α ) Γ ( β ) x α − 1 ( 1 − x ) β − 1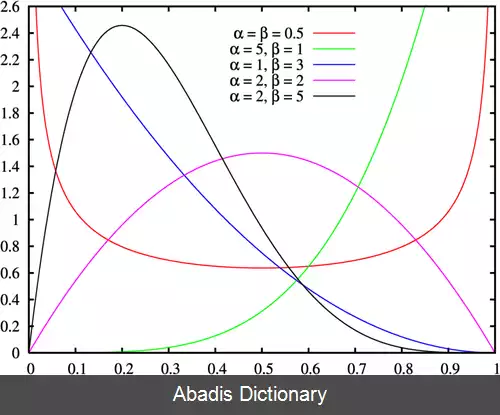
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفf ( x ) = x α − 1 ( 1 + x ) − α − β B ( α , β )
توزیع بتا نقش مهمی در تئوری آماره ترتیبی دارد. نتیجه بدین گونه است که توزیع kمین کوچک ترین مقدار از یک فضای نمونه nتایی از یک توزیع یکنواخت پیوسته معادل با یک توزیع بتا می باشد. نتیجه به صورت زیر خلاصه می گردد.
U ( k ) ∼ B e t a ( k , n + 1 − k )
موجک یک نوسان موج مانند با دامنه ای است که از صفر شروع می گردد، افزایش می یابد و سپس به صفر تقلیل می یابد. به طور معمول موجک ها را می توان به عنوان نوسان مختصری که به سرعت در حال فروپاشی هستند تجسم کرد. موجک ها می توانند برای استخراج اطلاعات از انواع مختلف داده استفاده گردند. از جمله این داده ها می توان به سیگنال ها و تصاویر صوتی اشاره نمود. به این ترتیب، موجک ها با این هدف ساخته می شوند تا ویژگی های خاصی داشته باشند که آن ها را قادر به پردازش سیگنال سازد. نکته ای که موجک ها را برجسته می سازد این است که آن ها هم در زمان و هم در فرکانس موضعی می باشند در حالی که تبدیل استاندارد فوریه تنها در فرکانس موضعی است. بنابراین، تبدیل استاندارد فوریه فقط برای فرایندهای ثابت قابل استفاده است در حالی که موجک ها برای فرآیندهای غیرثابت نیز قابل استفاده می باشند. موجک ها را می توان بر اساس توزیع بتا ساخت. موجک ساخته شده توسط توزیع بتا را می توان به عنوان یک طیف نرم از موج های هار مشاهده کرد که شکل آن با دو پارامتر α و β مشخص می گردد. [ ۱]
یکی از مهم ترین کاربردهای توزیع بتا استفاده از آن در آنالیز آماری بیزی توزیع دوجمله ای است. درواقع توزیع بتا به عنوان یک مدل برای احتمال موفقیت یک توزیع دوجمله ای استفاده می گردد، به این صورت که توزیع بتا به عنوان یک توزیع پیشین یا پسین برای آنالیز مورد استفاده قرار می گیرد. [ ۲]
f ( x ; α , β ) = x α − 1 ( 1 − x ) β − 1 ∫ 0 3 u α − 1 ( 1 − u ) β − 1 d u
= Γ ( α + β ) Γ ( α ) Γ ( β ) x α − 1 ( 1 − x ) β − 1

wiki: توزیع بتا
