توزیع احتمال شرطی اگر توزیع مشترک ( توزیع احتمال توام ) دو متغیر تصادفی X و Y را داشته باشیم، توزیع احتمال Y به شرط X ، توزیع احتمال Y است وقتی X دارای مقدار مشخصی باشد. اگر توزیع احتمال شرطی Y به شرط X یک توزیع پیوسته باشد، آنگاه تابع چگالی احتمال با نام تابع چگالی شرطی خوانده می شود.
امید ریاضی و واریانس در توزیع شرطی به ترتیب امید ریاضی شرطی و واریانس شرطی نام دارند.
برای متغیر های تصادفی گسسته توزیع احتمال شرطی به صورت زیر است:
p Y ( y ∣ X = x ) = P ( Y = y ∣ X = x ) = P ( X = x ∩ Y = y ) P ( X = x ) .
واضح است که P ( X=x ) > ۰.
رابطه زیر به دست آوردن توزیع X به شرط Y را از روی توزیع Y به شرط X نشان می دهد:
P ( Y = y ∣ X = x ) P ( X = x ) = P ( X = x ∩ Y = y ) = P ( X = x ∣ Y = y ) P ( Y = y ) .
به طور مشابه برای متغیرهای تصادفی پیوسته تابع چگالی احتمال Y به شرط X به صورت زیر نوشته می شود:
f Y ( y ∣ X = x ) = f X , Y ( x , y ) f X ( x ) ,
که در اینجا ( fX، Y ( x، y تابع چگالی مشترک X و Y را نشان می دهد و ( fX ( x تابع چگالی X را.
در اینجا نیز واضح است که ۰ < ( fX ( x
رابطه تابع چگالی شرطی X به شرط Y به صورت زیر خواهد بود:
f Y ( y ∣ X = x ) f X ( x ) = f X , Y ( x , y ) = f X ( x ∣ Y = y ) f Y ( y ) .
دو متغیر تصادفی X و Y مستقلند اگر و فقط اگر توزیع احتمال شرطی Y به شرط X برابر باشد با توزیع Y ( بدون مشروط کردن آن ) . یعنی:
در مورد متغیرهای تصادفی پیوسته رابطه بالا به صورت زیر خواهد بود:
به عنوان تابعی از y برای هر x داده شده ( P ( Y=y|X=x یک احتمال خواهد بود و جمع روی y ( یا انتگرال روی y در صورت پیوسته بودن توزیع ) ۱ خواهد شد. در حالی که به عنوان تابعی از x برای هر y داده شده رابطه فوق یک احتمال نخواهد بود و جمع روی x برابر با ۱ نخواهد شد.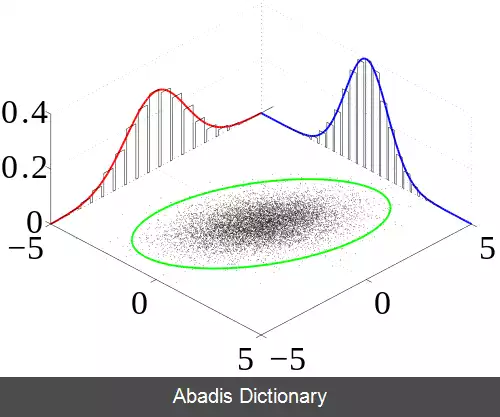
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفامید ریاضی و واریانس در توزیع شرطی به ترتیب امید ریاضی شرطی و واریانس شرطی نام دارند.
برای متغیر های تصادفی گسسته توزیع احتمال شرطی به صورت زیر است:
p Y ( y ∣ X = x ) = P ( Y = y ∣ X = x ) = P ( X = x ∩ Y = y ) P ( X = x ) .
واضح است که P ( X=x ) > ۰.
رابطه زیر به دست آوردن توزیع X به شرط Y را از روی توزیع Y به شرط X نشان می دهد:
P ( Y = y ∣ X = x ) P ( X = x ) = P ( X = x ∩ Y = y ) = P ( X = x ∣ Y = y ) P ( Y = y ) .
به طور مشابه برای متغیرهای تصادفی پیوسته تابع چگالی احتمال Y به شرط X به صورت زیر نوشته می شود:
f Y ( y ∣ X = x ) = f X , Y ( x , y ) f X ( x ) ,
که در اینجا ( fX، Y ( x، y تابع چگالی مشترک X و Y را نشان می دهد و ( fX ( x تابع چگالی X را.
در اینجا نیز واضح است که ۰ < ( fX ( x
رابطه تابع چگالی شرطی X به شرط Y به صورت زیر خواهد بود:
f Y ( y ∣ X = x ) f X ( x ) = f X , Y ( x , y ) = f X ( x ∣ Y = y ) f Y ( y ) .
دو متغیر تصادفی X و Y مستقلند اگر و فقط اگر توزیع احتمال شرطی Y به شرط X برابر باشد با توزیع Y ( بدون مشروط کردن آن ) . یعنی:
در مورد متغیرهای تصادفی پیوسته رابطه بالا به صورت زیر خواهد بود:
به عنوان تابعی از y برای هر x داده شده ( P ( Y=y|X=x یک احتمال خواهد بود و جمع روی y ( یا انتگرال روی y در صورت پیوسته بودن توزیع ) ۱ خواهد شد. در حالی که به عنوان تابعی از x برای هر y داده شده رابطه فوق یک احتمال نخواهد بود و جمع روی x برابر با ۱ نخواهد شد.

wiki: توزیع احتمال شرطی
