در ریاضیات، چندجمله ای های وابسته لژاندر جواب های متعارف:
از معادله زیر موسوم به معادله لژاندر هستند:
که در آن شاخص ℓ و m ( که اعداد صحیح هستند ) به عنوان مرتبه و درجه چند جمله ای لژاندر وابسته می باشند. این معادله دارای جواب های غیر صفر است و تنها در صورتی در غیر منفردند که اعداد صحیح ℓ و m در شرط 0 ≤ | m | ≤ | ℓ | صدق کنند. هنگامی که شاخص m زوج باشد، این تابع یک چند جمله ای است. هنگامی که m برابر صفر و ℓ مقداری صحیح باشد، این توابع با چندجمله ای های لژاندر معادلند. به طور کلی هرگاه ℓ و m اعداد صحیح هستند، راه حل ها معمولاً به عنوان «چندجمله ای های لژاندر وابسته» خوانده می شود، حتی زمانی که m مقداری فرد بوده و معادله یک چندجمله ای نباشد. به طور کلی رده عمومی این توابع با مقادیر واقعی یا مرکب دلخواه از ℓ و m توابع لژاندر هستند. در این حالت پارامترها معمولاً با حروف یونانی برچسب گذاری می شوند.
معادله دیفرانسیل معمولی لژاندر اغلب در فیزیک و سایر زمینه های فنی کاربرد دارد، به ویژه در زمان حل معادله لاپلاس ( و معادلات دیفرانسیل با مشتقات جزئی وابسته ) در مختصات کروی. توابع وابسته لژاندر نقشی حیاتی در تعریف هماهنگ های کروی دارد.
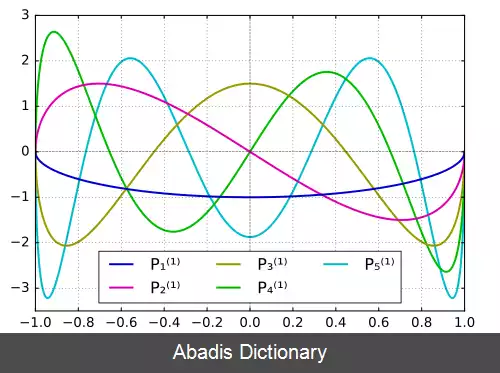
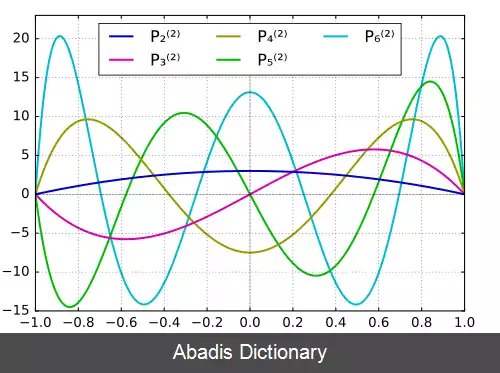
این توابع به صورت P ℓ m ( x ) که در آن بالانویس نشان دهنده ترتیب تابع است، و نه توان P. در تعریف دقیق تر، آن ها تعیین کننده مرتبه مشتق چندجمله ای های لژاندر هستند. ( m ≥ ۰ )
توابع توصیف شده در این معادله با مقادیر مشخص شده از پارامترهای ℓ و m معادله دیفرانسیل عمومی لژاندر را برآورده می کنند. پاسخ معادله لژاندر Pℓ با تفکیک m به شرح زیر است:[ ۱]
علاوه بر این، بر طبق فرمول رودریگز داریم:
که Pℓm را می توان به صورت زیر تعریف کرد:
این معادله گستره m را به ℓ ≤ m ≤ ℓ− محدود می کند. طبق تعریف Pℓ±m، حاصل عبارت فوق با جایگزینی m±، متناسب است. ضمن اینکه ضرایب توان در دو طرف معادله باید برابر باشد.
که از آن نتیجه می دهد ثابت تناسب برابر است با
بطوری که
نمادگذاری زیر نیز در نوشته ها استفاده می شود:[ ۲]
با فرض 0 ≤ m ≤ ℓ ، این توابع شرط تعامد را به ازای مقدار ثابت m برآورده می کنند:
که در آن δ k, ℓ همان تابع دلتای کرونیکر است.
همچنین، این توابع شرط تعامد را به ازای مقدار ثابت ℓ نیز برآورده می کنند: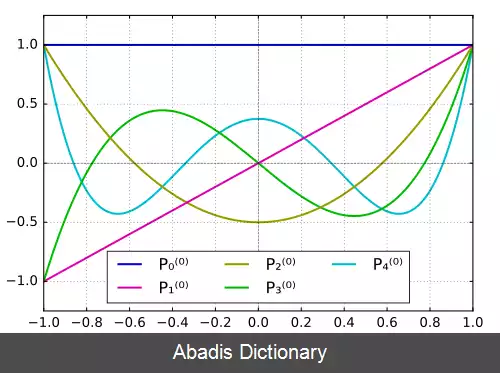
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاز معادله زیر موسوم به معادله لژاندر هستند:
که در آن شاخص ℓ و m ( که اعداد صحیح هستند ) به عنوان مرتبه و درجه چند جمله ای لژاندر وابسته می باشند. این معادله دارای جواب های غیر صفر است و تنها در صورتی در غیر منفردند که اعداد صحیح ℓ و m در شرط 0 ≤ | m | ≤ | ℓ | صدق کنند. هنگامی که شاخص m زوج باشد، این تابع یک چند جمله ای است. هنگامی که m برابر صفر و ℓ مقداری صحیح باشد، این توابع با چندجمله ای های لژاندر معادلند. به طور کلی هرگاه ℓ و m اعداد صحیح هستند، راه حل ها معمولاً به عنوان «چندجمله ای های لژاندر وابسته» خوانده می شود، حتی زمانی که m مقداری فرد بوده و معادله یک چندجمله ای نباشد. به طور کلی رده عمومی این توابع با مقادیر واقعی یا مرکب دلخواه از ℓ و m توابع لژاندر هستند. در این حالت پارامترها معمولاً با حروف یونانی برچسب گذاری می شوند.
معادله دیفرانسیل معمولی لژاندر اغلب در فیزیک و سایر زمینه های فنی کاربرد دارد، به ویژه در زمان حل معادله لاپلاس ( و معادلات دیفرانسیل با مشتقات جزئی وابسته ) در مختصات کروی. توابع وابسته لژاندر نقشی حیاتی در تعریف هماهنگ های کروی دارد.
این توابع به صورت P ℓ m ( x ) که در آن بالانویس نشان دهنده ترتیب تابع است، و نه توان P. در تعریف دقیق تر، آن ها تعیین کننده مرتبه مشتق چندجمله ای های لژاندر هستند. ( m ≥ ۰ )
توابع توصیف شده در این معادله با مقادیر مشخص شده از پارامترهای ℓ و m معادله دیفرانسیل عمومی لژاندر را برآورده می کنند. پاسخ معادله لژاندر Pℓ با تفکیک m به شرح زیر است:[ ۱]
علاوه بر این، بر طبق فرمول رودریگز داریم:
که Pℓm را می توان به صورت زیر تعریف کرد:
این معادله گستره m را به ℓ ≤ m ≤ ℓ− محدود می کند. طبق تعریف Pℓ±m، حاصل عبارت فوق با جایگزینی m±، متناسب است. ضمن اینکه ضرایب توان در دو طرف معادله باید برابر باشد.
که از آن نتیجه می دهد ثابت تناسب برابر است با
بطوری که
نمادگذاری زیر نیز در نوشته ها استفاده می شود:[ ۲]
با فرض 0 ≤ m ≤ ℓ ، این توابع شرط تعامد را به ازای مقدار ثابت m برآورده می کنند:
که در آن δ k, ℓ همان تابع دلتای کرونیکر است.
همچنین، این توابع شرط تعامد را به ازای مقدار ثابت ℓ نیز برآورده می کنند:



wiki: توابع وابسته لژاندر
