توابع نویل تتا نام خود را از اریک هرولد نویل گرفته است، [ ۱] این توابع به این شکل تعریف می شوند:[ ۲] [ ۳]
در اینجا K ( m ) انتگرال بیوی کامل نوع اول است، K ′ ( m ) = K ( 1 − m ) و q ( m ) = e − π K ′ ( m ) / K ( m ) نومِ بیضوی است.
توابع نویل تتا می توانند توسط توابع ژاکوبی تتا هم نمایش داده شوند[ ۴]
در اینجا z ′ = z / θ 3 ( 0 | τ ) 2 .
توابع نویل تتا با توابع بیضوی ژاکوبی مرتبط هستند. اگر p q ( u , m ) یک تابع بیضوی ژاکوبی باشد آنگاه:
اگر m = 0. 3 و z = 2. 5 را در تعاریف تابع نویل تتا جایگذاری کنیم به مقادیر پایین می رسیم.
• θ c ( 2. 5 , 0. 3 ) = − 0. 65900466676738154967 {\displaystyle \theta _{c} ( 2. 5, 0. 3 ) = - 0. 65900466676738154967} [ ۵]
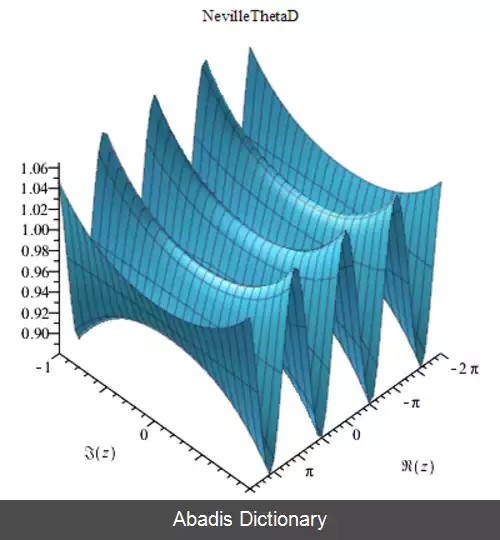
• θ d ( 2. 5 , 0. 3 ) = 0. 95182196661267561994 {\displaystyle \theta _{d} ( 2. 5, 0. 3 ) =0. 95182196661267561994}
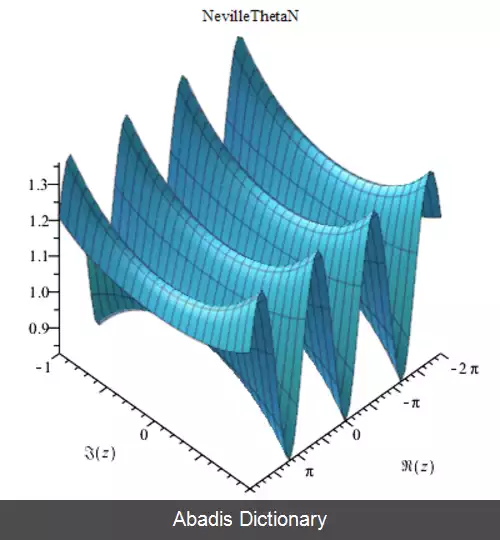
• θ n ( 2. 5 , 0. 3 ) = 1. 0526693354651613637 {\displaystyle \theta _{n} ( 2. 5, 0. 3 ) =1. 0526693354651613637}
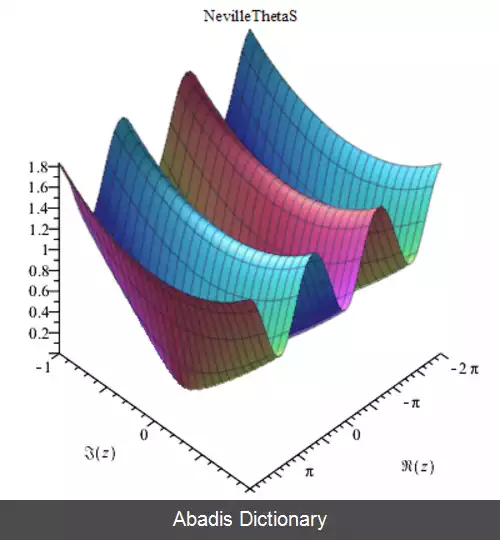
• θ s ( 2. 5 , 0. 3 ) = 0. 82086879524530400536 {\displaystyle \theta _{s} ( 2. 5, 0. 3 ) =0. 82086879524530400536}
• θ c ( z , m ) = θ c ( − z , m ) {\displaystyle \theta _{c} ( z, m ) =\theta _{c} ( - z, m ) }
• θ d ( z , m ) = θ d ( − z , m ) {\displaystyle \theta _{d} ( z, m ) =\theta _{d} ( - z, m ) }
• θ n ( z , m ) = θ n ( − z , m ) {\displaystyle \theta _{n} ( z, m ) =\theta _{n} ( - z, m ) }
• θ s ( z , m ) = − θ s ( − z , m ) {\displaystyle \theta _{s} ( z, m ) = - \theta _{s} ( - z, m ) }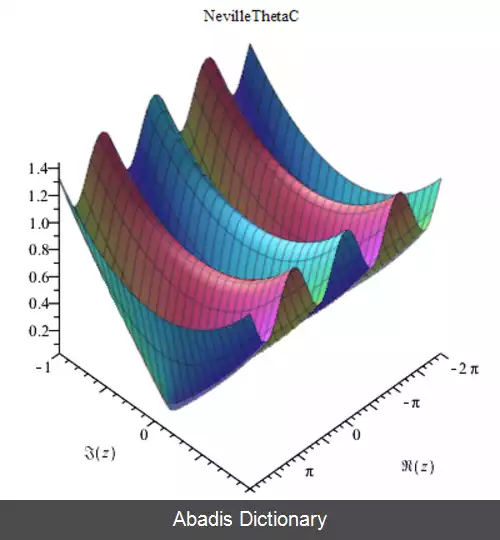
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر اینجا K ( m ) انتگرال بیوی کامل نوع اول است، K ′ ( m ) = K ( 1 − m ) و q ( m ) = e − π K ′ ( m ) / K ( m ) نومِ بیضوی است.
توابع نویل تتا می توانند توسط توابع ژاکوبی تتا هم نمایش داده شوند[ ۴]
در اینجا z ′ = z / θ 3 ( 0 | τ ) 2 .
توابع نویل تتا با توابع بیضوی ژاکوبی مرتبط هستند. اگر p q ( u , m ) یک تابع بیضوی ژاکوبی باشد آنگاه:
اگر m = 0. 3 و z = 2. 5 را در تعاریف تابع نویل تتا جایگذاری کنیم به مقادیر پایین می رسیم.
• θ c ( 2. 5 , 0. 3 ) = − 0. 65900466676738154967 {\displaystyle \theta _{c} ( 2. 5, 0. 3 ) = - 0. 65900466676738154967} [ ۵]
• θ d ( 2. 5 , 0. 3 ) = 0. 95182196661267561994 {\displaystyle \theta _{d} ( 2. 5, 0. 3 ) =0. 95182196661267561994}
• θ n ( 2. 5 , 0. 3 ) = 1. 0526693354651613637 {\displaystyle \theta _{n} ( 2. 5, 0. 3 ) =1. 0526693354651613637}
• θ s ( 2. 5 , 0. 3 ) = 0. 82086879524530400536 {\displaystyle \theta _{s} ( 2. 5, 0. 3 ) =0. 82086879524530400536}
• θ c ( z , m ) = θ c ( − z , m ) {\displaystyle \theta _{c} ( z, m ) =\theta _{c} ( - z, m ) }
• θ d ( z , m ) = θ d ( − z , m ) {\displaystyle \theta _{d} ( z, m ) =\theta _{d} ( - z, m ) }
• θ n ( z , m ) = θ n ( − z , m ) {\displaystyle \theta _{n} ( z, m ) =\theta _{n} ( - z, m ) }
• θ s ( z , m ) = − θ s ( − z , m ) {\displaystyle \theta _{s} ( z, m ) = - \theta _{s} ( - z, m ) }




wiki: توابع نویل تتا
