توابع معکوس مثلثاتی در ریاضیات، معکوس تابع های مثلثاتی اند که طبق تعریف تابع وارون، بُرد آن ها زیرمجموعهٔ دامنهٔ تابع اصلی دیگری است. از آنجایی که تابع های مثلثاتی هیچکدام یک به یک نیستند، برای همین برای اینکه وارون آن ها تابع بماند ( به ازای یک ورودی چند خروجی به دست نیاید ) باید آن ها را محدود کرد ( نگاه کنید به آزمون خط افقی ) .
برای نمونه اگر تعریف کنیم y = arcsin ( x ) یا به شکل دیگر y = s i n − 1 x آنگاه x = sin ( y ) است اما به ازای یک x یکتا می توان چندین y پیدا کرد که به ازای آن x = sin ( y ) شود، مانند y مساوی صفر، π و ۲π که به ازای همهٔ آن ها مقدار سینوس یا x برابر با صفر است و این به این معنی است که تابع وارون سینوس یا arcsin یا s i n − 1 x می تواند چندین جواب داشته باشد arcsin ( 0 ) = 0 , π , 2 π درحالی که این خلاف مفهوم تابع بودن است. برای همین برای تمامی تابع های وارون مثلثاتی محدودیت بُرد یا خروجی قرار می دهیم تا به ازای یک ورودی چندین خروجی نداشته باشند.
نمایش توابع معکوس مثلثاتی به فرم مشابه s i n − 1 x ( سینوس اینورس ) برای اولین بار توسط جان هرشل در سال ۱۸۱۳ به کار برده شد. این فرم را نباید با مقدار 1 sin x اشتباه گرفت؛ چرا که اولی به معنای تابع وارون ( گرفته شده از نماد y = f − 1 ( x ) ) و دومی به معنای عکس مقدار سینوس است.
همچنین Arc به معنای "قوس" یا کمانی است که مقدار نسبت مثلثاتی آن معلوم است.
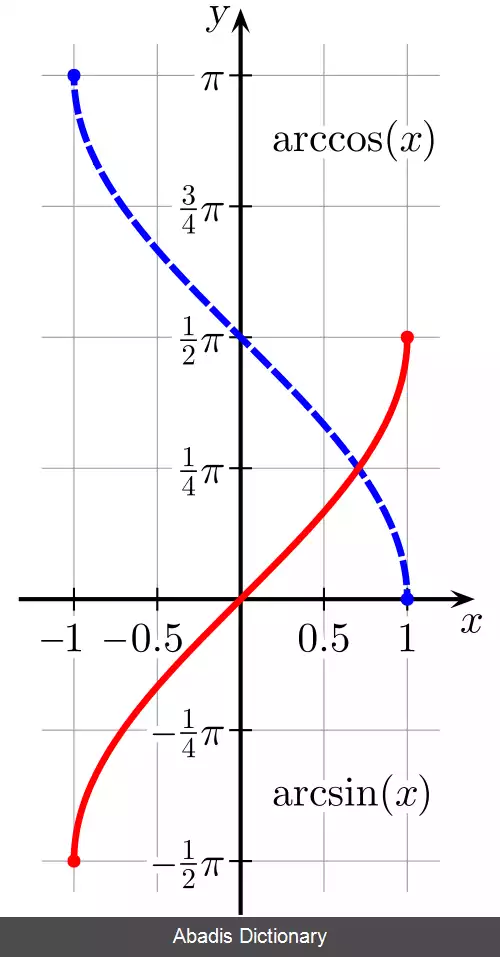
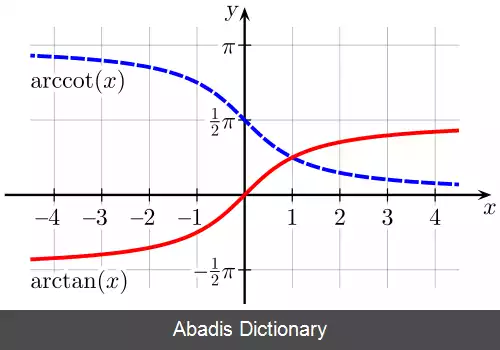
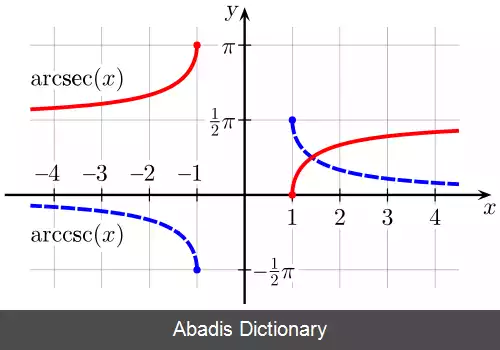
تابع های اصلی در جدول زیر آورده شده اند:
برخی تعاریف:
زاویه های مکمل:
ورودی های با علامت مخالف:
ورودی های وارون شده:
در صورتی که تنها بخشی از جدول سینوس را داشته باشیم:
هرگاه از ریشهٔ دوم یک عدد مختلط استفاده شد، باید ریشهٔ با بخش حقیقی مثبت را انتخاب کرد ( یا بخش موهومی مثبت، اگر خود آن، عدد حقیقی منفی بود ) .
با استفاده از رابطهٔ نیم - زاویه tan θ 2 = sin θ 1 + cos θ خواهیم داشت:
تابع های مثلثاتی در مجموعهٔ اعداد حقیقی، همگی تابع های متناوب اند و در بازه هایی به اندازهٔ ۲π مقدار همهٔ آن ها مرتب تکرار می شود. دورهٔ تناوب تابع های سینوس و کسکانت از ۲πk − π/۲ ( به ازای kهای عضو مجموعهٔ اعداد صحیح ) شروع می شود و در ۲πk + π/۲ تمام می شود، در نتیجه مقدار تابع میان بازهٔ ۲πk + π/۲ تا ۲πk + ۳π/۲ دوباره بر روی خودش باز می گردد. دورهٔ تناوب کسینوس و سکانت از ۲πk شروع می شود و در ۲πk + π تمام می شود و مقدار تابع در فاصلهٔ میان ۲πk + π تا ۲πk + ۲π دوباره بر روی خودش باز می گردد. دورهٔ تناوب تانژانت از ۲πk − π/۲ شروع می شود و در ۲πk + π/۲ تمام می شود و مقدار تابع به ازای بازه های ۲πk + π/۲ تا ۲πk + ۳π/۲ مرتب تکرار می شود. دورهٔ تناوب کتانژانت از ۲πk شروع می شود و در ۲πk + π تمام می شود، و تابع به ازای بازه های ۲πk + π تا ۲πk + ۲π بر روی خودش باز می گردد.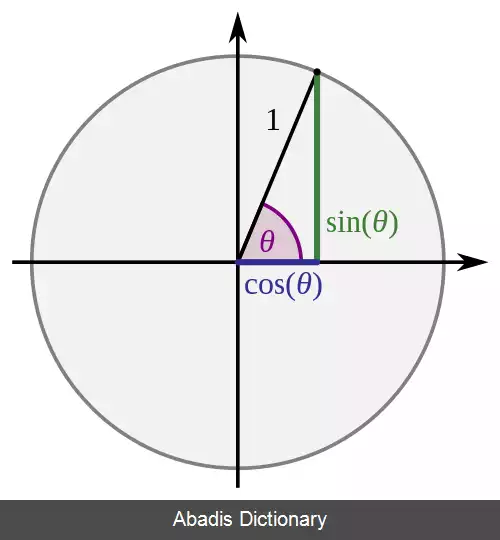
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرای نمونه اگر تعریف کنیم y = arcsin ( x ) یا به شکل دیگر y = s i n − 1 x آنگاه x = sin ( y ) است اما به ازای یک x یکتا می توان چندین y پیدا کرد که به ازای آن x = sin ( y ) شود، مانند y مساوی صفر، π و ۲π که به ازای همهٔ آن ها مقدار سینوس یا x برابر با صفر است و این به این معنی است که تابع وارون سینوس یا arcsin یا s i n − 1 x می تواند چندین جواب داشته باشد arcsin ( 0 ) = 0 , π , 2 π درحالی که این خلاف مفهوم تابع بودن است. برای همین برای تمامی تابع های وارون مثلثاتی محدودیت بُرد یا خروجی قرار می دهیم تا به ازای یک ورودی چندین خروجی نداشته باشند.
نمایش توابع معکوس مثلثاتی به فرم مشابه s i n − 1 x ( سینوس اینورس ) برای اولین بار توسط جان هرشل در سال ۱۸۱۳ به کار برده شد. این فرم را نباید با مقدار 1 sin x اشتباه گرفت؛ چرا که اولی به معنای تابع وارون ( گرفته شده از نماد y = f − 1 ( x ) ) و دومی به معنای عکس مقدار سینوس است.
همچنین Arc به معنای "قوس" یا کمانی است که مقدار نسبت مثلثاتی آن معلوم است.
تابع های اصلی در جدول زیر آورده شده اند:
برخی تعاریف:
زاویه های مکمل:
ورودی های با علامت مخالف:
ورودی های وارون شده:
در صورتی که تنها بخشی از جدول سینوس را داشته باشیم:
هرگاه از ریشهٔ دوم یک عدد مختلط استفاده شد، باید ریشهٔ با بخش حقیقی مثبت را انتخاب کرد ( یا بخش موهومی مثبت، اگر خود آن، عدد حقیقی منفی بود ) .
با استفاده از رابطهٔ نیم - زاویه tan θ 2 = sin θ 1 + cos θ خواهیم داشت:
تابع های مثلثاتی در مجموعهٔ اعداد حقیقی، همگی تابع های متناوب اند و در بازه هایی به اندازهٔ ۲π مقدار همهٔ آن ها مرتب تکرار می شود. دورهٔ تناوب تابع های سینوس و کسکانت از ۲πk − π/۲ ( به ازای kهای عضو مجموعهٔ اعداد صحیح ) شروع می شود و در ۲πk + π/۲ تمام می شود، در نتیجه مقدار تابع میان بازهٔ ۲πk + π/۲ تا ۲πk + ۳π/۲ دوباره بر روی خودش باز می گردد. دورهٔ تناوب کسینوس و سکانت از ۲πk شروع می شود و در ۲πk + π تمام می شود و مقدار تابع در فاصلهٔ میان ۲πk + π تا ۲πk + ۲π دوباره بر روی خودش باز می گردد. دورهٔ تناوب تانژانت از ۲πk − π/۲ شروع می شود و در ۲πk + π/۲ تمام می شود و مقدار تابع به ازای بازه های ۲πk + π/۲ تا ۲πk + ۳π/۲ مرتب تکرار می شود. دورهٔ تناوب کتانژانت از ۲πk شروع می شود و در ۲πk + π تمام می شود، و تابع به ازای بازه های ۲πk + π تا ۲πk + ۲π بر روی خودش باز می گردد.




wiki: توابع معکوس مثلثاتی
