رابطهٔ بین تنش برشی بحرانی τ C R S S وتنش برشی τ R S S
تنش برشی اعمال شده به صفحه ( resolved shear stress ) یا τ R S S که این پارامتر وابسته به دو زاویه است، اولی زاویهٔ بین بردار نرمال صفحه با جهت اعمال نیرو φ دومین زاویه، زاویهٔ بین جهت لغزش صفحه و جهت اعمال نیرو استλ. حال چرا τ R S S وابسته به این دو زاویه است زیرا تنش برشی برابر است با نیرو تقسیم بر واحد سطح در محاسبهٔ نیروی اعمال شده در صفحهٔ مورد نظر زاویهٔ دومی به کار برده می شود و در محاسبهٔ مساحت صفحه ای که به آن اعمال نیرو می شود زاویهٔ اولی استفاده می شود که رابطه آن به صورت زیر است
F D نیروی وارده به صفحهٔ لغزش A S مساحت صفحهٔ لغزش است
σ = F ÷ A
τ R S S = F D ÷ A S
F D = F × c o s ( λ )
A S = A ÷ c o s ( ϕ )
τ R S S = σ × c o s ( ϕ ) c o s ( λ ) [ ۱]
τ R S S = σ × m
در رابطه بالا m را ضریب اشمید[ ۲] می گوییم که همان وابستگی τ R S S ( resolved shear stress ) را به دو زاویه ϕ , λ نشان می دهد طبق این رابطه می توان فهمید که ماکزیمم مقدار تنش برشی در زاویه ۴۵درجه اتفاق می افتاد و در دو زاویه ۰، ۹۰ مقداررش صفر می شود
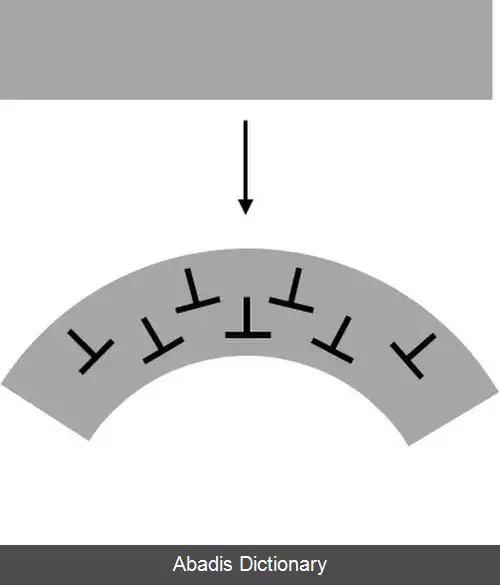
در اینجاست پارامتر دیگری را تعریف می کنیم به نام تنش برشی منعکس شده بحرانی τ C R S S ( critical resolved shear stress ) این پارامتر مقدار تنشی است که بتواند نابجایی را حرکت دهد ( ما می دانیم نابجایی در صفحات متراکم یا همان صفحات لغزش ( slip plane ) حرکت می کند ) حال خود این پارامتر به عوامل مختلفی بستگی دارد مانند ساختار کریستالی ماده، دما، پیوندهای بین اتمی ( یونی، کووالانسی و… )
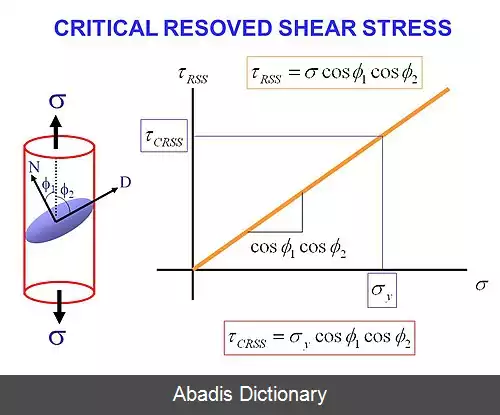
از آخرین روابطی که به دست آوردیم می فهمیم که σ , τ R S S با هم رابطهٔ خطی دارند که ضریب خط آنها m می باشد
نکتهٔ مهم اینجاست که تنش تسلیم σ y در تعریف آن داشتیم که باعث تغییر شکل پلاستیک ماده می شود و در تعریف تنش برشی بحرانی داشتیم که باعث τ C R S S باعث حرکت نابه جایی ها می شود بنابراین از آنجایی که حرکت نابه جایی ها دلیل تغییر شکل پلاستیک می باشد پس با توجه به شکل روبه رو نقطه ( σ y , τ R S S ) منطبق نمودار تنش و تنش برشی می باشند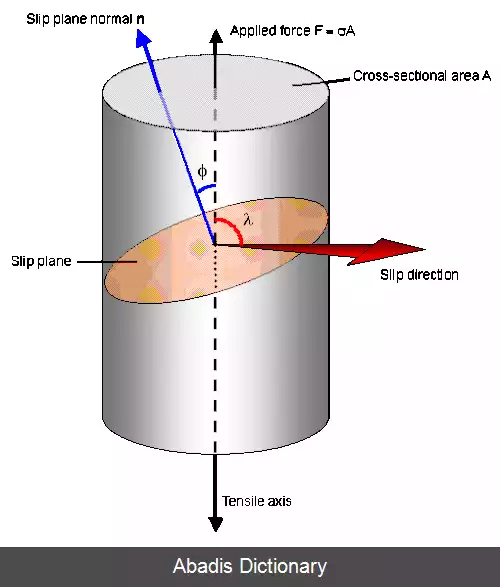

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتنش برشی اعمال شده به صفحه ( resolved shear stress ) یا τ R S S که این پارامتر وابسته به دو زاویه است، اولی زاویهٔ بین بردار نرمال صفحه با جهت اعمال نیرو φ دومین زاویه، زاویهٔ بین جهت لغزش صفحه و جهت اعمال نیرو استλ. حال چرا τ R S S وابسته به این دو زاویه است زیرا تنش برشی برابر است با نیرو تقسیم بر واحد سطح در محاسبهٔ نیروی اعمال شده در صفحهٔ مورد نظر زاویهٔ دومی به کار برده می شود و در محاسبهٔ مساحت صفحه ای که به آن اعمال نیرو می شود زاویهٔ اولی استفاده می شود که رابطه آن به صورت زیر است
F D نیروی وارده به صفحهٔ لغزش A S مساحت صفحهٔ لغزش است
σ = F ÷ A
τ R S S = F D ÷ A S
F D = F × c o s ( λ )
A S = A ÷ c o s ( ϕ )
τ R S S = σ × c o s ( ϕ ) c o s ( λ ) [ ۱]
τ R S S = σ × m
در رابطه بالا m را ضریب اشمید[ ۲] می گوییم که همان وابستگی τ R S S ( resolved shear stress ) را به دو زاویه ϕ , λ نشان می دهد طبق این رابطه می توان فهمید که ماکزیمم مقدار تنش برشی در زاویه ۴۵درجه اتفاق می افتاد و در دو زاویه ۰، ۹۰ مقداررش صفر می شود
در اینجاست پارامتر دیگری را تعریف می کنیم به نام تنش برشی منعکس شده بحرانی τ C R S S ( critical resolved shear stress ) این پارامتر مقدار تنشی است که بتواند نابجایی را حرکت دهد ( ما می دانیم نابجایی در صفحات متراکم یا همان صفحات لغزش ( slip plane ) حرکت می کند ) حال خود این پارامتر به عوامل مختلفی بستگی دارد مانند ساختار کریستالی ماده، دما، پیوندهای بین اتمی ( یونی، کووالانسی و… )
از آخرین روابطی که به دست آوردیم می فهمیم که σ , τ R S S با هم رابطهٔ خطی دارند که ضریب خط آنها m می باشد
نکتهٔ مهم اینجاست که تنش تسلیم σ y در تعریف آن داشتیم که باعث تغییر شکل پلاستیک ماده می شود و در تعریف تنش برشی بحرانی داشتیم که باعث τ C R S S باعث حرکت نابه جایی ها می شود بنابراین از آنجایی که حرکت نابه جایی ها دلیل تغییر شکل پلاستیک می باشد پس با توجه به شکل روبه رو نقطه ( σ y , τ R S S ) منطبق نمودار تنش و تنش برشی می باشند




