هدف الگوریتم تقریب کریستوفایدز ( به خاطر تلاش های نیکول کریستوفایدز نامگذاری شده است ) پیدا کردن راه حلی برای مثال هایی از مسئله فروشنده دوره گرد ( TSP ) است، به صورتی که وزن یال ها، نابرابری مثلثاتی را رعایت کنند. فرض کنید G = ( V , w ) مثالی از TSP باشد. به این معنی که G یک گراف کامل با یک سری رأس V با تابع وزن W است که به هر یال از G یک وزن واقعی و غیرمنفی نسبت می دهد.
به صورت شبه کد:
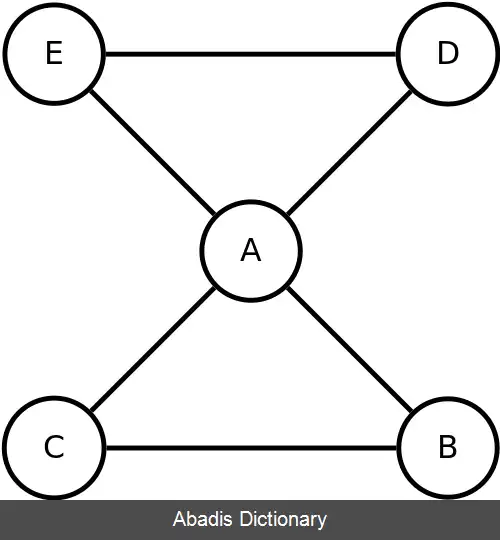
• درخت پوشای کمینه T {\displaystyle T} را از G {\displaystyle G} بسازید.
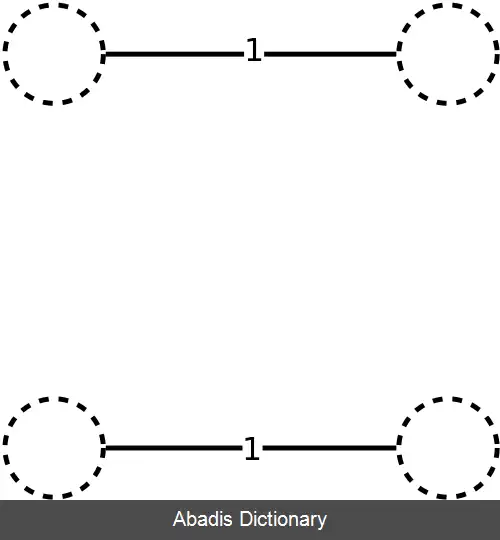
• فرض کنید O {\displaystyle O} شامل رئوسی با درجه فرد در درخت T {\displaystyle T} باشد. سپس تطابق کامل M {\displaystyle M} ، با کمترین وزن را در گراف کاملی شامل رئوس O {\displaystyle O} بیابید.
• یال های گراف M {\displaystyle M} و T {\displaystyle T} را با هم ترکیب کنید و گراف چندگانه H {\displaystyle H} را بسازید.
• یک دور اویلری در H {\displaystyle H} تشکیل دهید. ( H {\displaystyle H} اویلری است، زیرا گراف توسط رئوس با درجه زوج مرتبط شده است )
• چرخهٔ به دست آمده در قدم قبلی را با استفاده از نادیده گرفتن رئوس دیده شده، همیلتونی کنید.
هزینهٔ جواب درست شده توسط این روش بیشتر از ۳/۲ برابر جواب بهینه نیست اثبات: فرض بگیرید A گراف حاصل از مجموعهٔ یال های جواب بهینه مسئله TSP برای گراف G باشد به خاطر این که ( V, A ) همبند است، می توان در آن یک درخت پوشای کمینه مانند T یافت، و این که می دانیم w ( A ) ≥ w ( T ) و بعد فرض بگیرید B گراف حاصل از مجموعه یال های جواب بهینهٔ مسئلهٔ TSP برای گراف کامل روی رئوس O باشد به خاطر وجود ویژگی مثلثی بر روی یال های موجود گذر از راس های اضفه نمی توان هزینه را کم تر کند یعنی w ( A ) ≥ w ( B ) است. نشان می دهیم مچینگ کاملی وجود دارد که هزینهٔ آن حداکثر نصف w ( B ) باشد، پس w ( B ) /2 کران بالایی برای w ( M ) /2 می شود ( چون M مچینگ کامل کمینه است ) به این گونه که چون مقدار رئوس O زوج است، مچینگ کاملی در آن وجود دارد، فرض بگیرید e1, . . . , e2k مسیر اویلری در ( O , B ) باشد بدیهتا هم e1, . . . , e2k وهم e1, e3, . . . , e2k - 1 هرکدام مچینگ کامل هستند وزن حداقل یکی از آن ها بیشتر از w ( B ) /2 نیست پس w ( M ) +w ( T ) ≤ w ( A ) + w ( A ) /2 و به خاطر ویژگی مثلث به این روش تقریبی ۳/۲ است.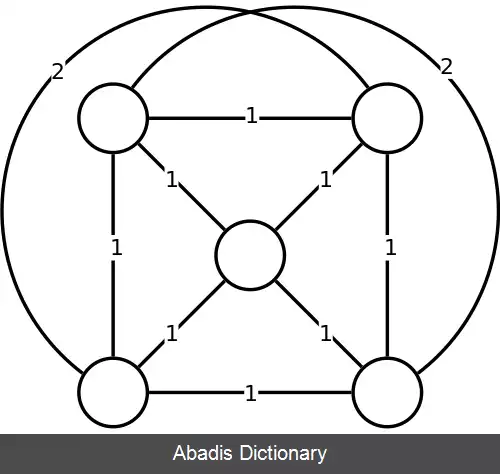
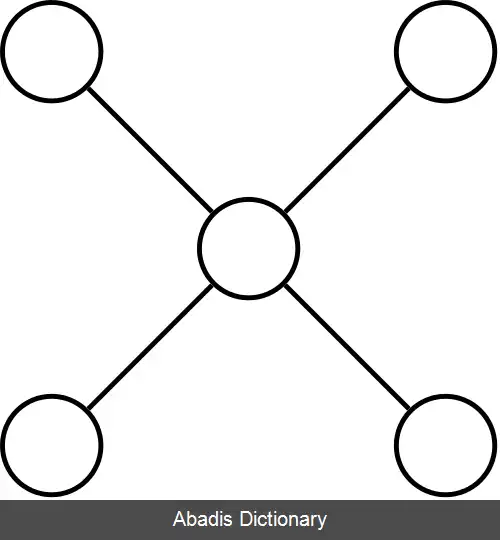
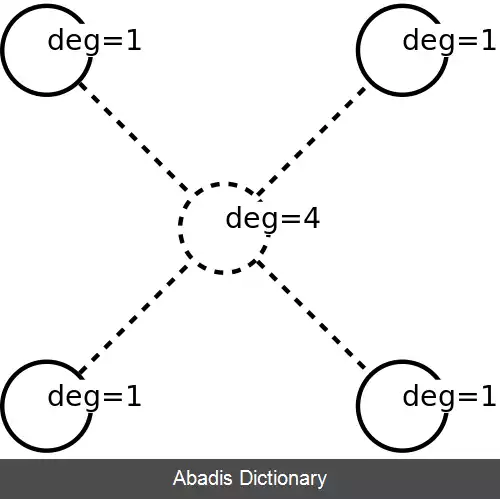
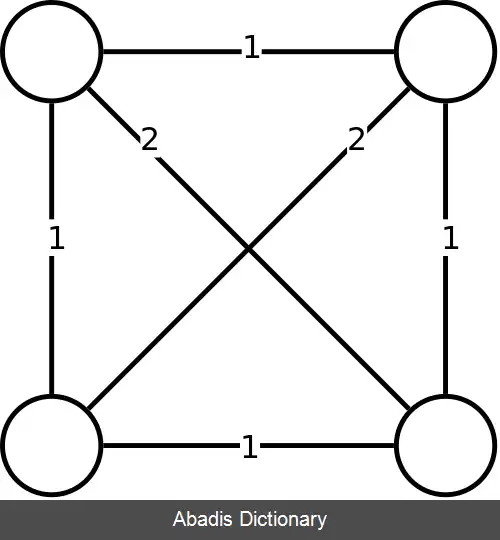
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه صورت شبه کد:
• درخت پوشای کمینه T {\displaystyle T} را از G {\displaystyle G} بسازید.
• فرض کنید O {\displaystyle O} شامل رئوسی با درجه فرد در درخت T {\displaystyle T} باشد. سپس تطابق کامل M {\displaystyle M} ، با کمترین وزن را در گراف کاملی شامل رئوس O {\displaystyle O} بیابید.
• یال های گراف M {\displaystyle M} و T {\displaystyle T} را با هم ترکیب کنید و گراف چندگانه H {\displaystyle H} را بسازید.
• یک دور اویلری در H {\displaystyle H} تشکیل دهید. ( H {\displaystyle H} اویلری است، زیرا گراف توسط رئوس با درجه زوج مرتبط شده است )
• چرخهٔ به دست آمده در قدم قبلی را با استفاده از نادیده گرفتن رئوس دیده شده، همیلتونی کنید.
هزینهٔ جواب درست شده توسط این روش بیشتر از ۳/۲ برابر جواب بهینه نیست اثبات: فرض بگیرید A گراف حاصل از مجموعهٔ یال های جواب بهینه مسئله TSP برای گراف G باشد به خاطر این که ( V, A ) همبند است، می توان در آن یک درخت پوشای کمینه مانند T یافت، و این که می دانیم w ( A ) ≥ w ( T ) و بعد فرض بگیرید B گراف حاصل از مجموعه یال های جواب بهینهٔ مسئلهٔ TSP برای گراف کامل روی رئوس O باشد به خاطر وجود ویژگی مثلثی بر روی یال های موجود گذر از راس های اضفه نمی توان هزینه را کم تر کند یعنی w ( A ) ≥ w ( B ) است. نشان می دهیم مچینگ کاملی وجود دارد که هزینهٔ آن حداکثر نصف w ( B ) باشد، پس w ( B ) /2 کران بالایی برای w ( M ) /2 می شود ( چون M مچینگ کامل کمینه است ) به این گونه که چون مقدار رئوس O زوج است، مچینگ کاملی در آن وجود دارد، فرض بگیرید e1, . . . , e2k مسیر اویلری در ( O , B ) باشد بدیهتا هم e1, . . . , e2k وهم e1, e3, . . . , e2k - 1 هرکدام مچینگ کامل هستند وزن حداقل یکی از آن ها بیشتر از w ( B ) /2 نیست پس w ( M ) +w ( T ) ≤ w ( A ) + w ( A ) /2 و به خاطر ویژگی مثلث به این روش تقریبی ۳/۲ است.






wiki: تقریب کریستوفایدز
