از تقریب های زاویه - کوچک می توان برای تقریب زدن مقادیر توابع مثلثاتی اصلی استفاده کرد، به شرطی که زاویه مورد نظر کوچک باشد و با رادیان اندازه گیری شود:
این تقریب ها در شاخه های از فیزیک و مهندسی از جمله مکانیک، الکترومغناطیس، نورشناسی، نقشه نگاری، اخترشناسی و علوم رایانه کاربردهای گسترده ای دارند. یک دلیل برای این امر این است که آنها می توانند معادلات دیفرانسیل را که نیازی به پاسخ با دقت مطلق ندارند، تا حد زیادی ساده کنند.
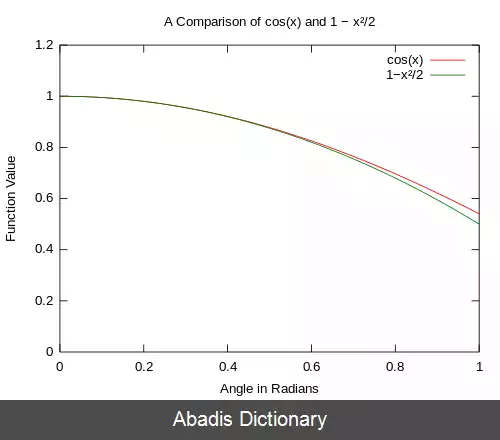
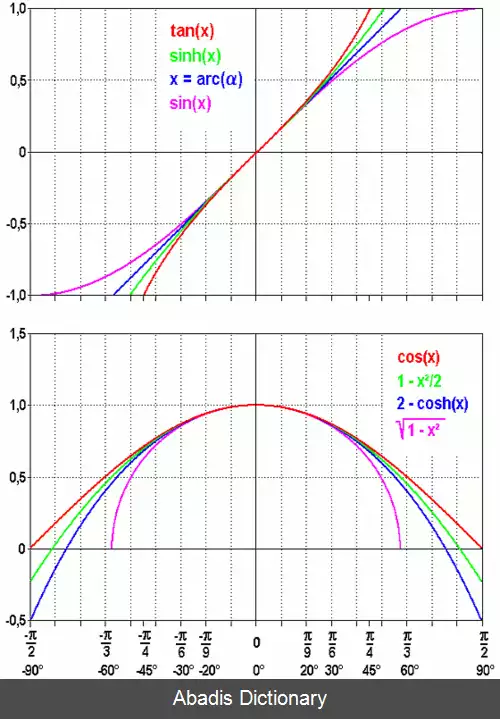
دقت تقریبی ها در زیر در شکل ۱ و شکل ۲ دیده می شود. با نزدیک شدن میزان زاویه به صفر، تفاوت تقریب و تابع اصلی نیز به ۰ نزدیک می شود.
بخش قرمز در سمت راست، d تفاوت بین طول وتر، H و در سمت مجاور، A می باشد. همان طور که نشان داده شده است، طول H و A تقریباً یکسان است، به این معنی که cos θ نزدیک به ۱ و است θ2/2 کمک می کند تا تر و تمیز دور قرمز.
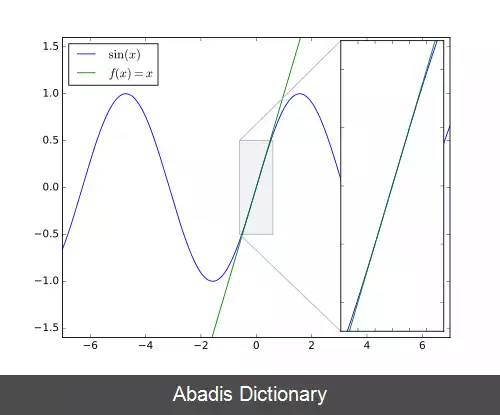
با استفاده از قضیه فشردگی، می توانیم این را ثابت کنیم lim θ → 0 sin ( θ ) θ = 1 ، که بیان رسمی تقریب sin ( θ ) ≈ θ برای مقادیر کوچک θ است.
بسط مَکلورن ( بسط تیلور در حدود ۰ ) از تابع مثلثاتی مربوطه[ ۱]
که θ زاویه در رادیان است. به عبارت واضح تر،
به راحتی مشاهده می شود که دومین جمله مهم ( مرتبه سوم ) به عنوان مکعب جمله اول سقوط می کند؛ بنابراین، حتی برای یک استدلال نه چندان کوچک مانند ۰٫۰۱، ارزش جمله دوم مهم تر در مرتبه ۶۹۹۴۱۰۰۰۰۰۰۰۰۰۰۰۰۰۰♠۰٫۰۰۰۰۰۱، یا 1/۷۰۰۴۱۰۰۰۰۰۰۰۰۰۰۰۰۰۰♠۱۰۰۰۰ اولین جمله است؛ بنابراین می توان با خیال راحت تخمین زد:
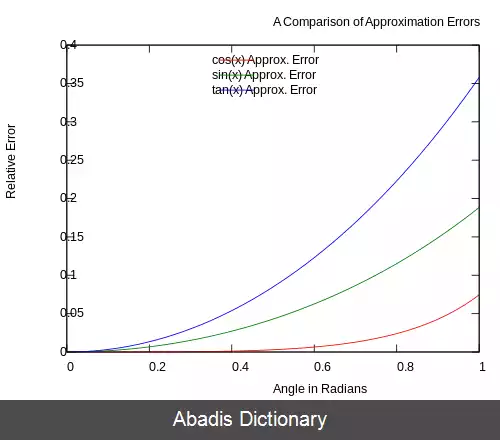
شکل ۳ خطاهای نسبی تقریب های زاویه کوچک را نشان می دهد. زاویه هایی که خطای نسبی بیش از ۱٪ است به شرح زیر است:
• cos θ ≈ ۱ حدود ۰٫۱۴۰۸ رادیان ( ۸٫۰۷° )
• tan θ ≈ θ حدود ۰٫۱۷۳۰ رادیان ( ۹٫۹۱° )
• sin θ ≈ θ حدود ۰٫۲۴۴۱ رادیان ( ۱۳٫۹۹° )
• cos θ ≈ ۱ − θ2/2 حدود ۰٫۶۶۲۰ رادیان ( ۳۷٫۹۳° )
قضیه های جمع و تفریق زاویه در صورت کوچک بودن یکی از زاویه ها ( β ≈ ۰ ) به موارد زیر کاهش می یابد:
در اخترشناسی، قطر زاویه ای یا زاویه فرورفته با تصویر یک جسم دور اغلب فقط چند ثانیه قوسی است، بنابراین برای تقریب زاویه کوچک مناسب است. اندازه خطی ( D ) با فرمول ساده به اندازه زاویه ای ( X ) و فاصله از ناظر ( d ) مربوط می شود: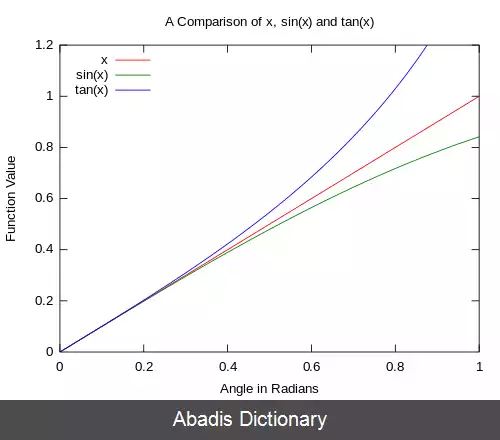
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین تقریب ها در شاخه های از فیزیک و مهندسی از جمله مکانیک، الکترومغناطیس، نورشناسی، نقشه نگاری، اخترشناسی و علوم رایانه کاربردهای گسترده ای دارند. یک دلیل برای این امر این است که آنها می توانند معادلات دیفرانسیل را که نیازی به پاسخ با دقت مطلق ندارند، تا حد زیادی ساده کنند.
دقت تقریبی ها در زیر در شکل ۱ و شکل ۲ دیده می شود. با نزدیک شدن میزان زاویه به صفر، تفاوت تقریب و تابع اصلی نیز به ۰ نزدیک می شود.
بخش قرمز در سمت راست، d تفاوت بین طول وتر، H و در سمت مجاور، A می باشد. همان طور که نشان داده شده است، طول H و A تقریباً یکسان است، به این معنی که cos θ نزدیک به ۱ و است θ2/2 کمک می کند تا تر و تمیز دور قرمز.
با استفاده از قضیه فشردگی، می توانیم این را ثابت کنیم lim θ → 0 sin ( θ ) θ = 1 ، که بیان رسمی تقریب sin ( θ ) ≈ θ برای مقادیر کوچک θ است.
بسط مَکلورن ( بسط تیلور در حدود ۰ ) از تابع مثلثاتی مربوطه[ ۱]
که θ زاویه در رادیان است. به عبارت واضح تر،
به راحتی مشاهده می شود که دومین جمله مهم ( مرتبه سوم ) به عنوان مکعب جمله اول سقوط می کند؛ بنابراین، حتی برای یک استدلال نه چندان کوچک مانند ۰٫۰۱، ارزش جمله دوم مهم تر در مرتبه ۶۹۹۴۱۰۰۰۰۰۰۰۰۰۰۰۰۰۰♠۰٫۰۰۰۰۰۱، یا 1/۷۰۰۴۱۰۰۰۰۰۰۰۰۰۰۰۰۰۰♠۱۰۰۰۰ اولین جمله است؛ بنابراین می توان با خیال راحت تخمین زد:
شکل ۳ خطاهای نسبی تقریب های زاویه کوچک را نشان می دهد. زاویه هایی که خطای نسبی بیش از ۱٪ است به شرح زیر است:
• cos θ ≈ ۱ حدود ۰٫۱۴۰۸ رادیان ( ۸٫۰۷° )
• tan θ ≈ θ حدود ۰٫۱۷۳۰ رادیان ( ۹٫۹۱° )
• sin θ ≈ θ حدود ۰٫۲۴۴۱ رادیان ( ۱۳٫۹۹° )
• cos θ ≈ ۱ − θ2/2 حدود ۰٫۶۶۲۰ رادیان ( ۳۷٫۹۳° )
قضیه های جمع و تفریق زاویه در صورت کوچک بودن یکی از زاویه ها ( β ≈ ۰ ) به موارد زیر کاهش می یابد:
در اخترشناسی، قطر زاویه ای یا زاویه فرورفته با تصویر یک جسم دور اغلب فقط چند ثانیه قوسی است، بنابراین برای تقریب زاویه کوچک مناسب است. اندازه خطی ( D ) با فرمول ساده به اندازه زاویه ای ( X ) و فاصله از ناظر ( d ) مربوط می شود:





wiki: تقریب زاویه کوچک
