مسئله نزدیکترین زوج نقاط یا نزدیکترین زوج یک مسئله از هندسه محاسباتی است که در آن در فضای متری n نقطه به عنوان ورودی گرفته می شود و زوج نقطه ای که کوتاه ترین فاصله بین آن دو وجود دارد، پیدا می شود. مسئله نزدیکترین زوج برای نقاط در صفحهٔ اقلیدسی[ ۱] از اولین مسائل هندسه بود که مطالعات سیستماتیک در نظریه پیچیدگی محاسباتی، الگوریتم های هندسه شد.
الگوریتم ساده، پیدا کردن فاصلهٔ همهٔ زوج نقاط و انتخاب کمینهٔ آن هاست که نیازمند زمانی از مرتبهٔ O ( n 2 ) است. به نظر می رسد مسئله در زمان O ( n l g n ) در فضای اقلیدسی با بعد ثابت d قابل حل باشد. در درخت تصمیم جبری مدل محاسبه الگوریتم با زمان O ( n l g n ) با توجه به کاهشی از مساله یکتایی عنصر بهینه است. در مدل محاسباتی چنین فرض می شود که تابع کف در زمان ثابت قابل محاسبه است و مساله می تواند در O ( n l g l g n ) حل شود. [ ۲] اگر در تابع کف از حالت تصادفی استفاده کنیم مسئله در O ( n ) نیز قابل حل است. [ ۳] [ ۴]
نزدیکترین زوج از نقاط با استتفاده از جستجوی جامع در نظریه پیچیدگی محاسباتی O ( n 2 ) قابل محاسبه است. برای این کار باید فاصلهٔ میان تمام n ( n − 1 ) 2 زوج نقطه را محاسبه کرده و زوجی را که کم ترین فاصله را دارند، انتحاب کنیم. شبه کد این الگوریتم در زیرمشاهده می شود. [ ۱]
minDist = infinity for i = 1 to length ( P ) - 1 for j = i + 1 to length ( P ) let p = P, q = P if dist ( p, q ) < minDist: minDist = dist ( p, q ) closestPair = ( p, q ) return closestPair حالت صفحه مسئله با استفاده از الگوریتم تقسیم و حل در زمان O ( n l o g n ) قابل حل است. رویه در زیر قابل مشاهده است.
• نقاط را براساس مولفهٔ x {\displaystyle x} آن ها مرتب می کنیم.
• مجموعهٔ نقاط را با استفاده از یک خط عمودی به صورت x = x m i d {\displaystyle x=x_{mid}} به دو زیرمجموعهٔ با اندازهٔ مساوی تقسیم می کنیم.
• مسئله را به صورت بازگشتی برای زیرمجموعه های راست و چپ حل می کنیم که کمینهٔ فاصله برای سمت راست و چپ به ترتیب به صورت d R m i n {\displaystyle d_{Rmin}} و d L m i n {\displaystyle d_{Lmin}} به دست می آید.
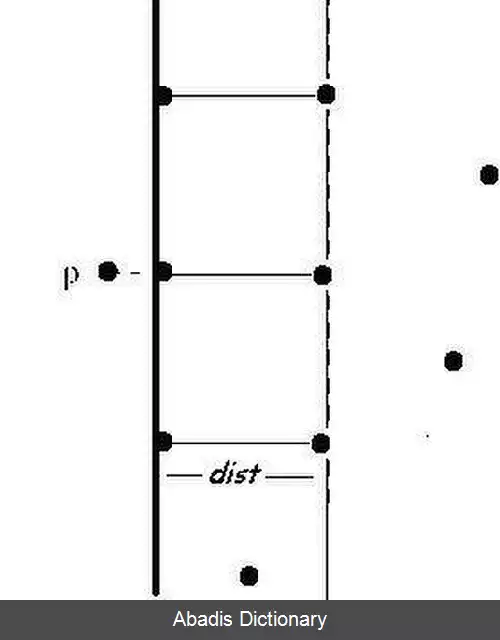
• کمینه فاصله بین نقاطی را که یکی شان در زیرمجموعهٔ سمت چپ قرار دارد و دیگری در زیرمجموعهٔ سمت راست انتخاب می کنیم و آن را d L R m i n {\displaystyle d_{LRmin}} می نامیم.
• جواب نهایی کمینه فاصله میان d L R m i n {\displaystyle d_{LRmin}} d L m i n {\displaystyle d_{Lmin}} d R m i n {\displaystyle d_{Rmin}} است.
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفالگوریتم ساده، پیدا کردن فاصلهٔ همهٔ زوج نقاط و انتخاب کمینهٔ آن هاست که نیازمند زمانی از مرتبهٔ O ( n 2 ) است. به نظر می رسد مسئله در زمان O ( n l g n ) در فضای اقلیدسی با بعد ثابت d قابل حل باشد. در درخت تصمیم جبری مدل محاسبه الگوریتم با زمان O ( n l g n ) با توجه به کاهشی از مساله یکتایی عنصر بهینه است. در مدل محاسباتی چنین فرض می شود که تابع کف در زمان ثابت قابل محاسبه است و مساله می تواند در O ( n l g l g n ) حل شود. [ ۲] اگر در تابع کف از حالت تصادفی استفاده کنیم مسئله در O ( n ) نیز قابل حل است. [ ۳] [ ۴]
نزدیکترین زوج از نقاط با استتفاده از جستجوی جامع در نظریه پیچیدگی محاسباتی O ( n 2 ) قابل محاسبه است. برای این کار باید فاصلهٔ میان تمام n ( n − 1 ) 2 زوج نقطه را محاسبه کرده و زوجی را که کم ترین فاصله را دارند، انتحاب کنیم. شبه کد این الگوریتم در زیرمشاهده می شود. [ ۱]
minDist = infinity for i = 1 to length ( P ) - 1 for j = i + 1 to length ( P ) let p = P, q = P if dist ( p, q ) < minDist: minDist = dist ( p, q ) closestPair = ( p, q ) return closestPair حالت صفحه مسئله با استفاده از الگوریتم تقسیم و حل در زمان O ( n l o g n ) قابل حل است. رویه در زیر قابل مشاهده است.
• نقاط را براساس مولفهٔ x {\displaystyle x} آن ها مرتب می کنیم.
• مجموعهٔ نقاط را با استفاده از یک خط عمودی به صورت x = x m i d {\displaystyle x=x_{mid}} به دو زیرمجموعهٔ با اندازهٔ مساوی تقسیم می کنیم.
• مسئله را به صورت بازگشتی برای زیرمجموعه های راست و چپ حل می کنیم که کمینهٔ فاصله برای سمت راست و چپ به ترتیب به صورت d R m i n {\displaystyle d_{Rmin}} و d L m i n {\displaystyle d_{Lmin}} به دست می آید.
• کمینه فاصله بین نقاطی را که یکی شان در زیرمجموعهٔ سمت چپ قرار دارد و دیگری در زیرمجموعهٔ سمت راست انتخاب می کنیم و آن را d L R m i n {\displaystyle d_{LRmin}} می نامیم.
• جواب نهایی کمینه فاصله میان d L R m i n {\displaystyle d_{LRmin}} d L m i n {\displaystyle d_{Lmin}} d R m i n {\displaystyle d_{Rmin}} است.


