در ریاضیات، دنبالهٔ هندسی یا تصاعد هندسی ( به انگلیسی: geometric progression ) به دنباله ای از اعداد گفته می شود که از جملهٔ اول به بعد، هر جمله برابر است با حاصل ضرب جملهٔ قبلی در یک عدد ثابتِ مخالف صفر و یک. به این عدد ثابت قدر نسبت تصاعد گفته می شود. برای نمونه دنبالهٔ ۲، ۶، ۱۸، ۵۴، … یک دنباله از اعداد با قدر نسبت ۳ است. مجموع اعداد یک دنبالهٔ هندسی را سری هندسی می نامند.
شکل کلی دنباله های هندسی به صورت زیر نوشته می شود:
بنابراین شکل کلی سری هندسی به صورت زیر خواهد بود:
در رابطه های بالا a جملهٔ اول دنباله و r ≠ ۰ قدر نسبت تصاعد می باشد.
n امین جملهٔ تصاعد هندسی با قدر نسبت r و جملهٔ اول a به صورت زیر نوشته می شود:
همچنین طبق معادلهٔ تفاضل برای تمامی n ≥ 1 می توان گفت:
رفتار جمله های یک دنبالهٔ هندسی تنها به قدر نسبت آن تصاعد وابسته است؛ چنانچه قدر نسبت تصاعد:
• مثبت باشد، جمله های بعدی دنباله همگی هم علامت جملهٔ اول خواهد بود.
• منفی باشد، جمله های بعدی دنباله به صورت یک در میان علامت مخالف خواهند داشت.
• بزرگتر از ۱ باشد، جمله های دنباله رشد نمایی به سمت مثبت بی نهایت خواهند داشت.
• ۱ باشد، دنباله ثابت خواهد بود.
• میان ۱ و ۱ - باشد به جزء صفر، جمله های بعدی دنباله به صفر میل می کند. ( اعداد سری هندسی به ترتیب کاهش می یابند و به صفر نزدیک می شوند؛ ولی هیچ گاه صفر نمی شود )
• ۱ - باشد، جمله های بعدی تشکیل یک دنبالهٔ متناوب را خواهند داد. ( اعداد به ترتیب یک در میان با تعویض علامت همراه هستند )
• کوچکتر از ۱ - باشد، قدر مطلق جمله های دنباله رشد نمایی خواهند داشت و هر یک از آن ها بسته به علامت به سمت مثبت یا منفی بی نهایت میل خواهند کرد.
در صورتی که در دنباله های هندسی، قدر نسبت برابر با ۰ یا ۱ یا ۱ - نباشد، در حالت کلی شاهد رشد نمایی به سمت مثبت یا منفی بی نهایت ( بسته به علامت جمله ها ) یا به سمت صفر خواهیم بود.
برای تشخیص دنباله هندسی دو جمله متوالی از دنباله هندسی را به هم تقسیم کنیم.
اگر به مقدار ثابتی رسیدیم. دنباله ما هندسی هست. مثال: آیا دنبال زیر هندسی است؟
جواب:
پس دنباله بالا هندسی است.
اگر سه جمله a , b , c ، سه جمله متوالی دنباله هندسی باشد. آنگاه رابطه زیر برقرار است:
b 2 = a c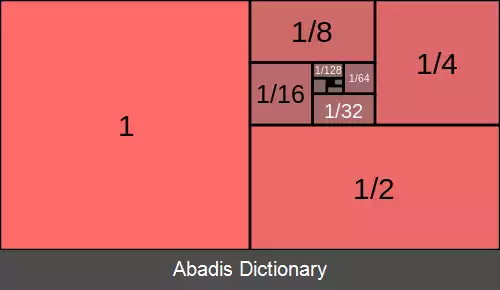
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفشکل کلی دنباله های هندسی به صورت زیر نوشته می شود:
بنابراین شکل کلی سری هندسی به صورت زیر خواهد بود:
در رابطه های بالا a جملهٔ اول دنباله و r ≠ ۰ قدر نسبت تصاعد می باشد.
n امین جملهٔ تصاعد هندسی با قدر نسبت r و جملهٔ اول a به صورت زیر نوشته می شود:
همچنین طبق معادلهٔ تفاضل برای تمامی n ≥ 1 می توان گفت:
رفتار جمله های یک دنبالهٔ هندسی تنها به قدر نسبت آن تصاعد وابسته است؛ چنانچه قدر نسبت تصاعد:
• مثبت باشد، جمله های بعدی دنباله همگی هم علامت جملهٔ اول خواهد بود.
• منفی باشد، جمله های بعدی دنباله به صورت یک در میان علامت مخالف خواهند داشت.
• بزرگتر از ۱ باشد، جمله های دنباله رشد نمایی به سمت مثبت بی نهایت خواهند داشت.
• ۱ باشد، دنباله ثابت خواهد بود.
• میان ۱ و ۱ - باشد به جزء صفر، جمله های بعدی دنباله به صفر میل می کند. ( اعداد سری هندسی به ترتیب کاهش می یابند و به صفر نزدیک می شوند؛ ولی هیچ گاه صفر نمی شود )
• ۱ - باشد، جمله های بعدی تشکیل یک دنبالهٔ متناوب را خواهند داد. ( اعداد به ترتیب یک در میان با تعویض علامت همراه هستند )
• کوچکتر از ۱ - باشد، قدر مطلق جمله های دنباله رشد نمایی خواهند داشت و هر یک از آن ها بسته به علامت به سمت مثبت یا منفی بی نهایت میل خواهند کرد.
در صورتی که در دنباله های هندسی، قدر نسبت برابر با ۰ یا ۱ یا ۱ - نباشد، در حالت کلی شاهد رشد نمایی به سمت مثبت یا منفی بی نهایت ( بسته به علامت جمله ها ) یا به سمت صفر خواهیم بود.
برای تشخیص دنباله هندسی دو جمله متوالی از دنباله هندسی را به هم تقسیم کنیم.
اگر به مقدار ثابتی رسیدیم. دنباله ما هندسی هست. مثال: آیا دنبال زیر هندسی است؟
جواب:
پس دنباله بالا هندسی است.
اگر سه جمله a , b , c ، سه جمله متوالی دنباله هندسی باشد. آنگاه رابطه زیر برقرار است:
b 2 = a c

wiki: تصاعد هندسی
