داده ساختار تریپ داده ساختاری است که در واقع از ترکیب دو داده ساختار درخت دودویی جستجو و هرم استفاده می کند.
قبل از توضیح این داده ساختار اندکی در مورد ایراد درخت دودویی جستجو و هرم توضیح می دهیم.
هرم دو نوع کلی دارد. هرم بیشینه و هرم کمینه. برای مثال هرم بیشینه درختی می باشد که هر پدری حداکثر دو فرزند دارد و مقدار کلید پدر از فرزندانش بیشتر می باشد. این داده ساختار به راحتی با آرایه قابل پیاده سازی می باشد. مهمترین مشکل این داده ساختار جستجوی یک عضو در آن می باشد. زیرا زمان اجرای آن خطی می شود؛ ولی درج عنصر در این داده ساختار از O ( lgn ) می باشد. حذف عنصر هم به دلیل اینکه نیاز به جستجو این عنصر داریم باز خطی می شود.
درخت دودویی جستجو یه درخت دودویی است که همهٔ کلیدهای گره های زیردرخت چپ هر گره آن با کلید k، کوچک تر از k و همهٔ کلیدهای گره های زیر درخت راست آن بزرگتر از k باشد.
عملیات فرهنگ داده ای شامل جستجو، درج و حذف در زمان اجرای O ( h ) انجام می دهد؛ که h همان ارتفاع درخت می باشد. ارتفاع درخت دودویی جستجو در حالت میانگین معادل lgn است؛ ولی ممکن است تا n هم پیش رود؛ بنابراین ضعف این داده ساختار مشخص شد. این در صورتی اتفاق می افتد که داده ها مثلاً به صورت مرتب شده در درخت دودویی جستجو درج بشوند. با تکنیک هایی مانند درخت قرمز و سیاه می توان کاری کرد که این درخت همواره در ارتفاع lgn بماند، ولی معمولاً پیاده سازی سختی دارند. به علاوه اینکه ضریت ثابت lgn در درخت قرمز و سیاه ممکن است خیلی بزرگ باشد.
تریپ تکنیکی دیگری می باشد برای اینکه ارتفاع درخت دودویی جستجو را با احتمال بالایی لگاریتمی نگه داریم. پیاده سازی آن هم بسیار ساده می باشد.
داده ساختار تریپ اولین بار در سال ۱۹۸۹ توسط سیسیلیا ر آراگون و ریموند سیدل معرفی شد.
در تریپ هر گره آن دارای دو کلید می باشد. گره ها بر اساس یکی از این کلیدها به ترتیب درخت دودویی جستجو درج می شوند، بعد از درج هر گره، به کلید دوم این گره نگاه می کنیم؛ و این سؤال پرسیده می شود که آیا بر اساس مقدار کلید دوم ترتیب هرم بیشینه در این داده ساختار رعایت شده است یا نه؟ اگر کلید دوم این گره از پدرش کمتر بود که کار تمام است. یعنی درج این عنصر به پایان رسیده است؛ ولی اگه مقدار کلید دومش از همتای پدرش بیشتر بود عمل دوران را تا وقتی که ترتیب هرم بیشینه درست شود انجام می دهیم. مقدار کلید دوم هم از قبل معلوم نیست و هنگام ایجاد گره مورد نظر به صورت تصادفی مقدار دهی می شود و به این کلید اولویت عددی هم می گویند. این طوری با احتمال خیلی قوی درخت دودویی جستجو لگاریتمی می ماند.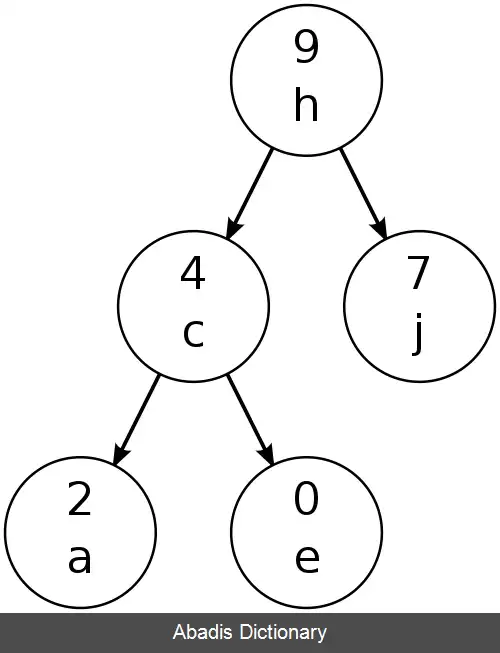
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفقبل از توضیح این داده ساختار اندکی در مورد ایراد درخت دودویی جستجو و هرم توضیح می دهیم.
هرم دو نوع کلی دارد. هرم بیشینه و هرم کمینه. برای مثال هرم بیشینه درختی می باشد که هر پدری حداکثر دو فرزند دارد و مقدار کلید پدر از فرزندانش بیشتر می باشد. این داده ساختار به راحتی با آرایه قابل پیاده سازی می باشد. مهمترین مشکل این داده ساختار جستجوی یک عضو در آن می باشد. زیرا زمان اجرای آن خطی می شود؛ ولی درج عنصر در این داده ساختار از O ( lgn ) می باشد. حذف عنصر هم به دلیل اینکه نیاز به جستجو این عنصر داریم باز خطی می شود.
درخت دودویی جستجو یه درخت دودویی است که همهٔ کلیدهای گره های زیردرخت چپ هر گره آن با کلید k، کوچک تر از k و همهٔ کلیدهای گره های زیر درخت راست آن بزرگتر از k باشد.
عملیات فرهنگ داده ای شامل جستجو، درج و حذف در زمان اجرای O ( h ) انجام می دهد؛ که h همان ارتفاع درخت می باشد. ارتفاع درخت دودویی جستجو در حالت میانگین معادل lgn است؛ ولی ممکن است تا n هم پیش رود؛ بنابراین ضعف این داده ساختار مشخص شد. این در صورتی اتفاق می افتد که داده ها مثلاً به صورت مرتب شده در درخت دودویی جستجو درج بشوند. با تکنیک هایی مانند درخت قرمز و سیاه می توان کاری کرد که این درخت همواره در ارتفاع lgn بماند، ولی معمولاً پیاده سازی سختی دارند. به علاوه اینکه ضریت ثابت lgn در درخت قرمز و سیاه ممکن است خیلی بزرگ باشد.
تریپ تکنیکی دیگری می باشد برای اینکه ارتفاع درخت دودویی جستجو را با احتمال بالایی لگاریتمی نگه داریم. پیاده سازی آن هم بسیار ساده می باشد.
داده ساختار تریپ اولین بار در سال ۱۹۸۹ توسط سیسیلیا ر آراگون و ریموند سیدل معرفی شد.
در تریپ هر گره آن دارای دو کلید می باشد. گره ها بر اساس یکی از این کلیدها به ترتیب درخت دودویی جستجو درج می شوند، بعد از درج هر گره، به کلید دوم این گره نگاه می کنیم؛ و این سؤال پرسیده می شود که آیا بر اساس مقدار کلید دوم ترتیب هرم بیشینه در این داده ساختار رعایت شده است یا نه؟ اگر کلید دوم این گره از پدرش کمتر بود که کار تمام است. یعنی درج این عنصر به پایان رسیده است؛ ولی اگه مقدار کلید دومش از همتای پدرش بیشتر بود عمل دوران را تا وقتی که ترتیب هرم بیشینه درست شود انجام می دهیم. مقدار کلید دوم هم از قبل معلوم نیست و هنگام ایجاد گره مورد نظر به صورت تصادفی مقدار دهی می شود و به این کلید اولویت عددی هم می گویند. این طوری با احتمال خیلی قوی درخت دودویی جستجو لگاریتمی می ماند.

wiki: تریپ
