در ریاضیات، ترکیب تابع یک نگاشت نقطه به نقطه از یک تابع به تابعی دیگر است برای تولید تابعی سوم. برای مثال دو تابع g : X → Y و تابع f : Y → Z می توانند ترکیب شوند و حاصل تابعی خواهد بود که مقدار x در X را به مقدار f ( g ( x ) ) در Z نگاشت می کند. به طور شهودی، اگر z حاصل تابع f از y باشد و y حاصل تابع g از x باشد، بنابراین z حاصل تابعی از x است.
تابع حاصل که به صورت f ∘ g : X → Z نماد می شود - که در بسیاری از منابع شامل این مقاله به صورت f ∘ g : X → Y نیز نوشته می شود - برای تمام xهای عضو X به صورت ( f ∘ g ) ( x ) = f ( g ( x ) ) تعریف می شود. نماد f ∘ g به صورت های "f در دایره f"، "g دور g"، "ترکیب g با g"، "f بعد از g"، "f به دنبال f" و "g ی f" و "g اُ f"نیز خوانده می شود. مشتق ترکیب توابع مشتق پذیر از طریق قاعده زنجیره ای بدست می آید. مشتق های مراتب بالاتر از چنین توابعی از رابطهٔ فادی برونو به دست می آیند.
• شرکت پذیری
ترکیب تابع همیشه شرکت پذیر است. به این معنا که اگر g، f و h سه تابع با دامنه و برد مناسب باشند، در اینصورت f ∘ ( g ∘ h ) = ( f ∘ g ) ∘ h، که در اینجا پرانتز به این معناست که عمل ترکیب ابتدا بر روی دو تابع داخل پرانتز صورت می گیرد. بنابراین چون محل قرارگیری پرانتزها در حاصل نهایی ترکیب تأثیری ندارد، می توان آن ها را بدون پیش آمد هیچ ابهامی حذف کرد.
• خاصیت جابه جایی
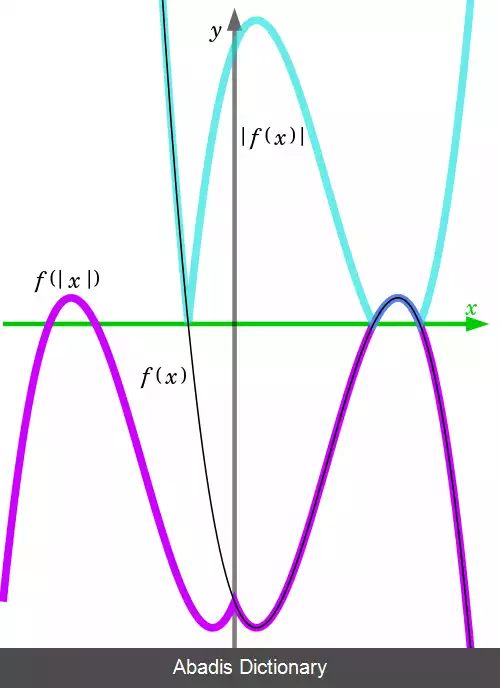
گفته می شود دو تابع f و g با یکدیگر خاصیت جابه جایی دارند اگر g ∘ f = f ∘ g. در کل، ترکیب توابع تعویض پذیر نخواهند بود. تعویض پذیری یک خاصیت ویژه است که توابع مخصوصی دارای آن می باشند و در موقعیت های خاص اتفاق می افتد. برای مثال، |x| + 3 = |x + 3| فقط زمانی صادق است که x ≥ 0 .
به عنوان مثال فرض کنید ارتفاع یک هواپیما در زمان t توسط تابع h ( t ) تعیین می شود، و تراکم اکسیژن درون هواپیما در ارتفاع x توسط تابع c ( x ) تعیین می شود. بنابراین تابع ( ( c ∘ h ) ( t ) میزان تراکم اکسیژن درون هواپیما در زمان t را تعریف می کند.
مقاله اصلی: تابع مکرر اگر Y ⊆ X ، تابع f : X → Y می تواند با خودش ترکیب شود. این ترکیب در بعضی مواقع با f 2 نشان داده می شود. بنابراین:
ترکیب بیش از یک بار یک تابع با خودش، تابع مکرر نامیده می شود.
خواص ترکیب تابع:
• f ∘ f n = f n ∘ f = f n + 1 {\displaystyle f\circ f^{n}=f^{n}\circ f=f^{n+1}} برای n های طبیعی
• بنابر تعریف: f 0 = i d D ( f ) {\displaystyle f^{0}=id_{D ( f ) }} ( تابع همانی در دامنهٔ f )
• اگر تابع f : X → X {\displaystyle f\colon X\rightarrow X} ، تابع وارون داشته باشد، توان های منفی تابع f − k {\displaystyle f^{ - k}\, } ( k > 0 ) {\displaystyle ( k> 0 ) } ، به صورت توان تابع وارون f {\displaystyle f} تعریف می شوند.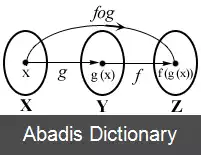
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتابع حاصل که به صورت f ∘ g : X → Z نماد می شود - که در بسیاری از منابع شامل این مقاله به صورت f ∘ g : X → Y نیز نوشته می شود - برای تمام xهای عضو X به صورت ( f ∘ g ) ( x ) = f ( g ( x ) ) تعریف می شود. نماد f ∘ g به صورت های "f در دایره f"، "g دور g"، "ترکیب g با g"، "f بعد از g"، "f به دنبال f" و "g ی f" و "g اُ f"نیز خوانده می شود. مشتق ترکیب توابع مشتق پذیر از طریق قاعده زنجیره ای بدست می آید. مشتق های مراتب بالاتر از چنین توابعی از رابطهٔ فادی برونو به دست می آیند.
• شرکت پذیری
ترکیب تابع همیشه شرکت پذیر است. به این معنا که اگر g، f و h سه تابع با دامنه و برد مناسب باشند، در اینصورت f ∘ ( g ∘ h ) = ( f ∘ g ) ∘ h، که در اینجا پرانتز به این معناست که عمل ترکیب ابتدا بر روی دو تابع داخل پرانتز صورت می گیرد. بنابراین چون محل قرارگیری پرانتزها در حاصل نهایی ترکیب تأثیری ندارد، می توان آن ها را بدون پیش آمد هیچ ابهامی حذف کرد.
• خاصیت جابه جایی
گفته می شود دو تابع f و g با یکدیگر خاصیت جابه جایی دارند اگر g ∘ f = f ∘ g. در کل، ترکیب توابع تعویض پذیر نخواهند بود. تعویض پذیری یک خاصیت ویژه است که توابع مخصوصی دارای آن می باشند و در موقعیت های خاص اتفاق می افتد. برای مثال، |x| + 3 = |x + 3| فقط زمانی صادق است که x ≥ 0 .
به عنوان مثال فرض کنید ارتفاع یک هواپیما در زمان t توسط تابع h ( t ) تعیین می شود، و تراکم اکسیژن درون هواپیما در ارتفاع x توسط تابع c ( x ) تعیین می شود. بنابراین تابع ( ( c ∘ h ) ( t ) میزان تراکم اکسیژن درون هواپیما در زمان t را تعریف می کند.
مقاله اصلی: تابع مکرر اگر Y ⊆ X ، تابع f : X → Y می تواند با خودش ترکیب شود. این ترکیب در بعضی مواقع با f 2 نشان داده می شود. بنابراین:
ترکیب بیش از یک بار یک تابع با خودش، تابع مکرر نامیده می شود.
خواص ترکیب تابع:
• f ∘ f n = f n ∘ f = f n + 1 {\displaystyle f\circ f^{n}=f^{n}\circ f=f^{n+1}} برای n های طبیعی
• بنابر تعریف: f 0 = i d D ( f ) {\displaystyle f^{0}=id_{D ( f ) }} ( تابع همانی در دامنهٔ f )
• اگر تابع f : X → X {\displaystyle f\colon X\rightarrow X} ، تابع وارون داشته باشد، توان های منفی تابع f − k {\displaystyle f^{ - k}\, } ( k > 0 ) {\displaystyle ( k> 0 ) } ، به صورت توان تابع وارون f {\displaystyle f} تعریف می شوند.


wiki: ترکیب تابع
