در جبر خطی ترانهاده ( به انگلیسی: Transpose ) یک ماتریس مانند A ماتریس دیگری است که با نماد AT ( به شکل های دیگر A′، Atr یا tA نوشته می شود ) مشخص شده و نسبت به ماتریس A دارای تفاوت با تعریف زیر است: i × j = j × i
به عبارت دیگر باید هنگام نوشتن ترانهاده هر ماتریسی سطرهای ماتریس را به شکل ستون نوشت و ستون های ماتریس را به شکل سطر؛
در واقع یک ماتریس n×m اگر ترانهاده شود یک ماتریس m×n خواهد بود. ترانهاده یک عدد همان عدد است.
• T = . {\displaystyle {\begin{bmatrix}1& 2\end{bmatrix}}^{\mathrm {T} }\!\!\; \!=\, {\begin{bmatrix}1\\2\end{bmatrix}}. }
• T = . {\displaystyle {\begin{bmatrix}1& 2\\3& 4\end{bmatrix}}^{\mathrm {T} }\!\!\; \!=\, {\begin{bmatrix}1& 3\\2& 4\end{bmatrix}}. }
• T = . {\displaystyle {\begin{bmatrix}1& 2\\3& 4\\5& 6\end{bmatrix}}^{\mathrm {T} }\!\!\; \!=\, {\begin{bmatrix}1& 3& 5\\2& 4& 6\end{bmatrix}}. \; }
برای دو ماتریس دلخواه A و B و عدد C خواص زیر صدق می کند
• ( A T ) T = A {\displaystyle \left ( \mathbf {A} ^{\mathrm {T} }\right ) ^{\mathrm {T} }=\mathbf {A} \quad \, }
• ( A + B ) T = A T + B T {\displaystyle ( \mathbf {A} +\mathbf {B} ) ^{\mathrm {T} }=\mathbf {A} ^{\mathrm {T} }+\mathbf {B} ^{\mathrm {T} }\, }
• ( A B ) T = B T A T {\displaystyle \left ( \mathbf {AB} \right ) ^{\mathrm {T} }=\mathbf {B} ^{\mathrm {T} }\mathbf {A} ^{\mathrm {T} }\, }
• ماتریس مربعی A وارون پذیر است اگر و فقط اگر AT وارون پذیر باشد
• ( c A ) T = c A T {\displaystyle ( c\mathbf {A} ) ^{\mathrm {T} }=c\mathbf {A} ^{\mathrm {T} }\, }
• det ( A T ) = det ( A ) {\displaystyle \det ( \mathbf {A} ^{\mathrm {T} } ) =\det ( \mathbf {A} ) \, }
• ضرب داخلی دو ماتریس a و b می توان به شکل زیر محاسبه شود.
که در نمادگذاری اینشتینai bi نوشته می شود.
• ( A T ) − 1 = ( A − 1 ) T {\displaystyle ( \mathbf {A} ^{\mathrm {T} } ) ^{ - 1}= ( \mathbf {A} ^{ - 1} ) ^{\mathrm {T} }\, }
• اگر A یک ماتریس مربعی باشد مقدار ویژه این ماتریس برابر مقدار ویژه ماتریس ترانهاده آن است.
ماتریس مربعی در صورتی ماتریس متقارن نامید می شود که ترانهاده اش با خودش برابر باشد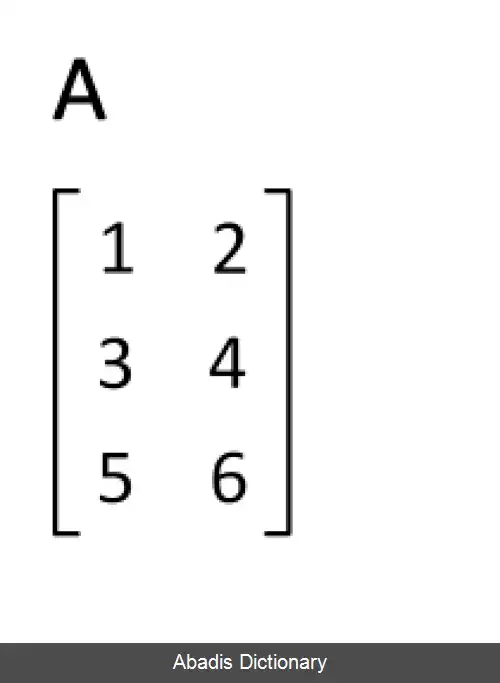
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه عبارت دیگر باید هنگام نوشتن ترانهاده هر ماتریسی سطرهای ماتریس را به شکل ستون نوشت و ستون های ماتریس را به شکل سطر؛
در واقع یک ماتریس n×m اگر ترانهاده شود یک ماتریس m×n خواهد بود. ترانهاده یک عدد همان عدد است.
• T = . {\displaystyle {\begin{bmatrix}1& 2\end{bmatrix}}^{\mathrm {T} }\!\!\; \!=\, {\begin{bmatrix}1\\2\end{bmatrix}}. }
• T = . {\displaystyle {\begin{bmatrix}1& 2\\3& 4\end{bmatrix}}^{\mathrm {T} }\!\!\; \!=\, {\begin{bmatrix}1& 3\\2& 4\end{bmatrix}}. }
• T = . {\displaystyle {\begin{bmatrix}1& 2\\3& 4\\5& 6\end{bmatrix}}^{\mathrm {T} }\!\!\; \!=\, {\begin{bmatrix}1& 3& 5\\2& 4& 6\end{bmatrix}}. \; }
برای دو ماتریس دلخواه A و B و عدد C خواص زیر صدق می کند
• ( A T ) T = A {\displaystyle \left ( \mathbf {A} ^{\mathrm {T} }\right ) ^{\mathrm {T} }=\mathbf {A} \quad \, }
• ( A + B ) T = A T + B T {\displaystyle ( \mathbf {A} +\mathbf {B} ) ^{\mathrm {T} }=\mathbf {A} ^{\mathrm {T} }+\mathbf {B} ^{\mathrm {T} }\, }
• ( A B ) T = B T A T {\displaystyle \left ( \mathbf {AB} \right ) ^{\mathrm {T} }=\mathbf {B} ^{\mathrm {T} }\mathbf {A} ^{\mathrm {T} }\, }
• ماتریس مربعی A وارون پذیر است اگر و فقط اگر AT وارون پذیر باشد
• ( c A ) T = c A T {\displaystyle ( c\mathbf {A} ) ^{\mathrm {T} }=c\mathbf {A} ^{\mathrm {T} }\, }
• det ( A T ) = det ( A ) {\displaystyle \det ( \mathbf {A} ^{\mathrm {T} } ) =\det ( \mathbf {A} ) \, }
• ضرب داخلی دو ماتریس a و b می توان به شکل زیر محاسبه شود.
که در نمادگذاری اینشتینai bi نوشته می شود.
• ( A T ) − 1 = ( A − 1 ) T {\displaystyle ( \mathbf {A} ^{\mathrm {T} } ) ^{ - 1}= ( \mathbf {A} ^{ - 1} ) ^{\mathrm {T} }\, }
• اگر A یک ماتریس مربعی باشد مقدار ویژه این ماتریس برابر مقدار ویژه ماتریس ترانهاده آن است.
ماتریس مربعی در صورتی ماتریس متقارن نامید می شود که ترانهاده اش با خودش برابر باشد

wiki: ترانهاده
