در تحلیل گره، مدار با استفاده از ولتاژ گره ها نسبت به یک گرۀ مرجع که زمین نامیده می شود تحلیل می شود.
• گره های مدار را شماره گذاری کنید.
• یک گره را به عنوان گرۀ مرجع انتخاب کنید.
• جریان شاخه ها را بر اساس تفاضل ولتاژ دو سر گره بخش بر امپدانس آن بنویسید.
• معادلات قانون جریان کیرشهف را برای گره ها به جز در گره مرجع بنویسید [ ۱] .
• دستگاه معادلات بدست آمده را حل کنید.
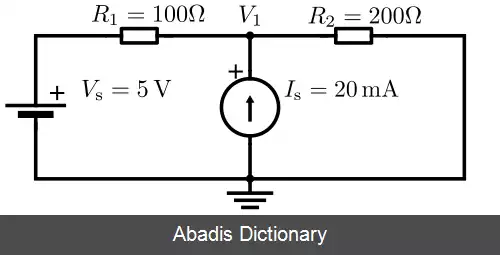
با استفاده از قانون جریان کیرشهف داریم:
V 1 − V S R 1 + V 1 R 2 − I S = 0
که از آن V۱ چنین بدست می آید:
V 1 = ( V S R 1 + I S ) ( 1 R 1 + 1 R 2 )
با جایگذاری مقادیر داده شده خواهیم داشت:
V 1 = ( 5 V 100 Ω + 20 mA ) ( 1 100 Ω + 1 200 Ω ) ≈ 4. 667 V
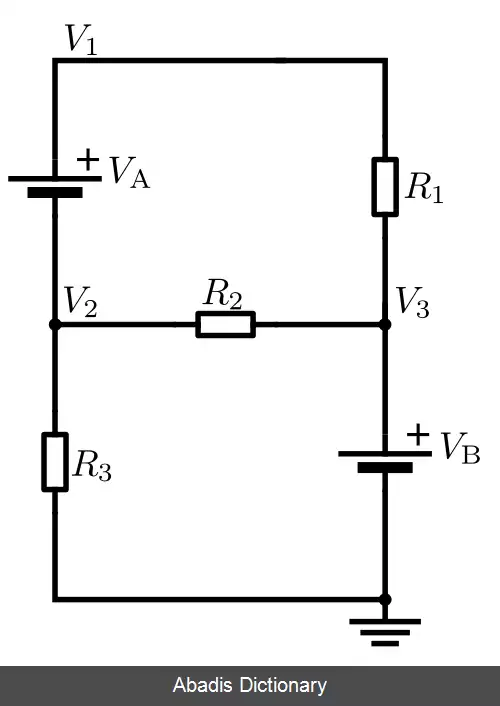
معادلات این مثال به شکل زیر خواهد بود:
{ V 1 − V B R 1 + V 2 − V B R 2 + V 2 R 3 = 0 V 1 = V 2 + V A
که از آن نتیجه خواهد شد:
V 2 = ( R 1 + R 2 ) R 3 V B − R 2 R 3 V A ( R 1 + R 2 ) R 3 + R 1 R 2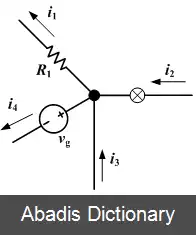
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• گره های مدار را شماره گذاری کنید.
• یک گره را به عنوان گرۀ مرجع انتخاب کنید.
• جریان شاخه ها را بر اساس تفاضل ولتاژ دو سر گره بخش بر امپدانس آن بنویسید.
• معادلات قانون جریان کیرشهف را برای گره ها به جز در گره مرجع بنویسید [ ۱] .
• دستگاه معادلات بدست آمده را حل کنید.
با استفاده از قانون جریان کیرشهف داریم:
V 1 − V S R 1 + V 1 R 2 − I S = 0
که از آن V۱ چنین بدست می آید:
V 1 = ( V S R 1 + I S ) ( 1 R 1 + 1 R 2 )
با جایگذاری مقادیر داده شده خواهیم داشت:
V 1 = ( 5 V 100 Ω + 20 mA ) ( 1 100 Ω + 1 200 Ω ) ≈ 4. 667 V
معادلات این مثال به شکل زیر خواهد بود:
{ V 1 − V B R 1 + V 2 − V B R 2 + V 2 R 3 = 0 V 1 = V 2 + V A
که از آن نتیجه خواهد شد:
V 2 = ( R 1 + R 2 ) R 3 V B − R 2 R 3 V A ( R 1 + R 2 ) R 3 + R 1 R 2



wiki: تحلیل گره
