در ریاضیات و فیزیک، تجزیه و تحلیل چند مقیاسی ( که روش مقیاس های چندگانه نیز نامیده می شود ) شامل تکنیک هایی است که برای ساختن تقریب های با اعتبار یکسان برای حل مسائل اختلالی استفاده می شود، این روش هم برای مقادیر کوچک و هم برای مقادیر بزرگ متغیرهای مستقل قابل استفاده است. این کار با تعریف متغیرهای مستقل جدید به نام متغییرهای مقیاسی سریع و آهسته انجام می شود و با این متغیرها، مانند متغییرهای مستقل رفتار می شود. این متغییرها به ما در فرایند حل مسائل اختلالی، آزادی عمل می دهد که بتوان جملات سکیولار ( جملات ناخواسته ای که منجر به واگرایی جواب های تقریبی مسئله می شوند ) را حذف کرد. همچنین قیدهایی را برای حل تقریبی ایجاد می کند که به آنها شرایط حل پذیری می گویند.
بررسی های ریاضی در دهه ۱۹۸۰ پشتیبانی قوی تری بر حسب تبدیل مختصات و منیفولدهای ثابت، برای مدل سازی چند مقیاسی فراهم می کنند ( برای مثال، منیفولد مرکزی و منیفولد آهسته را ببینید ) .
به عنوان یک مثال ساده برای تجزیه و تحلیل چند مقیاسی، معادله دافینگ بدون میرایی و بدون نیروی وادارنده را در نظر بگیرید:[ ۱] d 2 y d t 2 + y + ε y 3 = 0 , y ( 0 ) = 1 , d y d t ( 0 ) = 0 , که یک معادله دیفرانسیل معمولی مرتبه دوم است و یک نوسانگر غیرخطی را توصیف می کند. جواب y ( t ) برای مقادیر کوچک پارامتر غیرخطی ε ( ۰< ε ≪ ۱ ) جستجو می کنیم. معادله دافینگ نامیرایی خود یک سیستم همیلتونی است: d p d t = − ∂ H ∂ q , d q d t = + ∂ H ∂ p , with H = 1 2 p 2 + 1 2 q 2 + 1 4 ε q 4 , با q = y ( t ) و p = dy / dt. در نتیجه، H همیلتونی ( p , q ) یک کمیت پایستار است که برابر با H است = ½ + ¼ ε برای شرایط اولیه داده شده. این بدان معناست که هم y و هم dy / dt باید محدود شوند: | y ( t ) | ≤ 1 + 1 2 ε and | d y d t | ≤ 1 + 1 2 ε for all t . جواب اختلالی یک سری اختلال رایج برای این مسئله به صورت بسط زیر است y ( t ) = y 0 ( t ) + ε y 1 ( t ) + O ( ε 2 ) که با جایگزین کردن آن در معادله دافینگ نامیرا و سپس تطبیق توان های ε سیستم معادلات زیر بدست می آید: d 2 y 0 d t 2 + y 0 = 0 , d 2 y 1 d t 2 + y 1 = − y 0 3 . که با حل این دستگاه برای شرایط اولیه مسئله، رابطهٔ زیر نتیجه خواهد شد: y ( t ) = cos ( t ) + ε + O ( ε 2 ) . توجه داشته باشید که آخرین جملهٔ داخل کروشه، یک جملهٔ سکیولار است: که با زمان | t | به صورت خطی رشد می کند. به طور مشخص، برای زمان هایی از مرتبهٔ t = O ( ε − 1 ) ، این جمله از مرتبهٔ O ( 1 ) است و بنابراین از نظر بزرگی هم مرتبه با اولین جملهٔ عبارت خواهد بود. به دلیل وجود این نوع جملات در جواب اختلالی، این سری دیگر بسط مجانبی جواب مسئله نیست. روش مقیاس های چندگانه برای ساختن جوابی که فراتر از مرتبهٔ t = O ( ϵ − 1 ) معتبر باشد، از روش تحلیل مقیاس چندگانه استفاده می شود. متغیر مقیاس آهسته t 1 را به صورت زیر تعریف می کنیم: t 1 = ε t و فرض کنید که جواب y ( t ) دارای بسط اختلالی زیر است که هم به t و هم به t 1 وابسته است: y ( t ) = Y 0 ( t , t 1 ) + ε Y 1 ( t , t 1 ) + ⋯ . بنابراین: d y d t = ( ∂ Y 0 ∂ t + d t 1 d t ∂ Y 0 ∂ t 1 ) + ε ( ∂ Y 1 ∂ t + d t 1 d t ∂ Y 1 ∂ t 1 ) + ⋯ = ∂ Y 0 ∂ t + ε ( ∂ Y 0 ∂ t 1 + ∂ Y 1 ∂ t ) + O ( ε 2 ) , با استفاده از dt 1 / dt = ε. خواهیم داشت: d 2 y d t 2 = ∂ 2 Y 0 ∂ t 2 + ε ( 2 ∂ 2 Y 0 ∂ t ∂ t 1 + ∂ 2 Y 1 ∂ t 2 ) + O ( ε 2 ) . پس جواب های مرتبه صفر و مرتبه اول اختلالی - چند مقیاسی برای معادله دافینگ خواهد بود: ∂ 2 Y 0 ∂ t 2 + Y 0 = 0 , ∂ 2 Y 1 ∂ t 2 + Y 1 = − Y 0 3 − 2 ∂ 2 Y 0 ∂ t ∂ t 1 . راه حل برای مسئله مرتبه صفر راه حل کلی زیر وجود دارد: Y 0 ( t , t 1 ) = A ( t 1 ) e + i t + A ∗ ( t 1 ) e − i t , که A ( t 1 ) دامنه مختلط برای جواب مرتبه صفر Y 0 ( t , t 1 ) است. حال برای جواب مرتبه اول، نیرویی وابسته به زمان در سمت راست معادله دیفرانسیل دوم ظاهر می شود که برابر است با: e + i t − A 3 e + 3 i t + c . c . که در آن cc نشان دهنده مزدوج مختلط عبارت های قبلی است. از ایجاد جملات سکولار می توان با تحمیل شرط حل پذیری در دامنه A ( t 1 ) که هنوز نامشخص است جلوگیری کرد. − 3 A 2 A ∗ − 2 i d A d t 1 = 0. جواب شرط حل پذیری، همچنین شرایط اولیه y ( 0 ) = ۱ و dy/dt ( 0 ) = ۰ را برآورده می کند، یعنی: A = 1 2 exp ( 3 8 i t 1 ) . در نتیجه، جواب تقریبی با تجزیه و تحلیل چند مقیاسی عبارت است y ( t ) = cos + O ( ε ) , با استفاده از t1 = εt که تا مرتبه εt = O ( 1 ) اعتبار دارد. این با تغییرات غیرخطی فرکانس که ( وابستگی فرکانس به دامنه ) با استفاده از روش لیندستد - پوانکاره بدست می آید مطابقت دارد. این جواب تا زمان اعتبار دارد که زمان سپری شده برای سیستم از مرتبهٔ t = O ( ϵ − 2 ) باشد. جوابهای مرتبه های بالاتر - با استفاده از روش مقیاس های چندگانه - نیاز به تعریف متغییرهای مقیاسی آهستهٔ اضافی دارد، یعنی t2 = ε2 t, t3 = ε3 t و به همین ترتیب. با این حال باید توجه داشت که تعریف متغییرهای جدید می تواند ابهامات را در بسط اختلالی جواب بوجود آورد که لازم است با احتیاط با آن برخورد کرد ( به ( Kevorkian و Cole 1996 ) ؛ ( Bender و Orszag 1999 ) مراجعه کنید ) . [ ۲]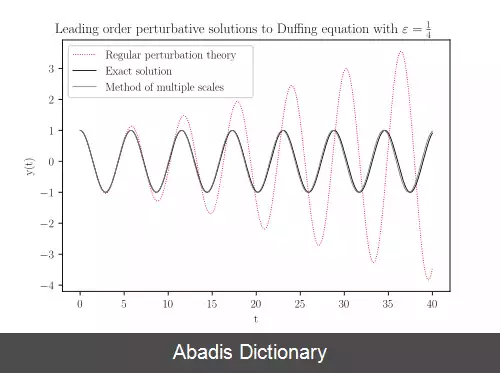
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبررسی های ریاضی در دهه ۱۹۸۰ پشتیبانی قوی تری بر حسب تبدیل مختصات و منیفولدهای ثابت، برای مدل سازی چند مقیاسی فراهم می کنند ( برای مثال، منیفولد مرکزی و منیفولد آهسته را ببینید ) .
به عنوان یک مثال ساده برای تجزیه و تحلیل چند مقیاسی، معادله دافینگ بدون میرایی و بدون نیروی وادارنده را در نظر بگیرید:[ ۱] d 2 y d t 2 + y + ε y 3 = 0 , y ( 0 ) = 1 , d y d t ( 0 ) = 0 , که یک معادله دیفرانسیل معمولی مرتبه دوم است و یک نوسانگر غیرخطی را توصیف می کند. جواب y ( t ) برای مقادیر کوچک پارامتر غیرخطی ε ( ۰< ε ≪ ۱ ) جستجو می کنیم. معادله دافینگ نامیرایی خود یک سیستم همیلتونی است: d p d t = − ∂ H ∂ q , d q d t = + ∂ H ∂ p , with H = 1 2 p 2 + 1 2 q 2 + 1 4 ε q 4 , با q = y ( t ) و p = dy / dt. در نتیجه، H همیلتونی ( p , q ) یک کمیت پایستار است که برابر با H است = ½ + ¼ ε برای شرایط اولیه داده شده. این بدان معناست که هم y و هم dy / dt باید محدود شوند: | y ( t ) | ≤ 1 + 1 2 ε and | d y d t | ≤ 1 + 1 2 ε for all t . جواب اختلالی یک سری اختلال رایج برای این مسئله به صورت بسط زیر است y ( t ) = y 0 ( t ) + ε y 1 ( t ) + O ( ε 2 ) که با جایگزین کردن آن در معادله دافینگ نامیرا و سپس تطبیق توان های ε سیستم معادلات زیر بدست می آید: d 2 y 0 d t 2 + y 0 = 0 , d 2 y 1 d t 2 + y 1 = − y 0 3 . که با حل این دستگاه برای شرایط اولیه مسئله، رابطهٔ زیر نتیجه خواهد شد: y ( t ) = cos ( t ) + ε + O ( ε 2 ) . توجه داشته باشید که آخرین جملهٔ داخل کروشه، یک جملهٔ سکیولار است: که با زمان | t | به صورت خطی رشد می کند. به طور مشخص، برای زمان هایی از مرتبهٔ t = O ( ε − 1 ) ، این جمله از مرتبهٔ O ( 1 ) است و بنابراین از نظر بزرگی هم مرتبه با اولین جملهٔ عبارت خواهد بود. به دلیل وجود این نوع جملات در جواب اختلالی، این سری دیگر بسط مجانبی جواب مسئله نیست. روش مقیاس های چندگانه برای ساختن جوابی که فراتر از مرتبهٔ t = O ( ϵ − 1 ) معتبر باشد، از روش تحلیل مقیاس چندگانه استفاده می شود. متغیر مقیاس آهسته t 1 را به صورت زیر تعریف می کنیم: t 1 = ε t و فرض کنید که جواب y ( t ) دارای بسط اختلالی زیر است که هم به t و هم به t 1 وابسته است: y ( t ) = Y 0 ( t , t 1 ) + ε Y 1 ( t , t 1 ) + ⋯ . بنابراین: d y d t = ( ∂ Y 0 ∂ t + d t 1 d t ∂ Y 0 ∂ t 1 ) + ε ( ∂ Y 1 ∂ t + d t 1 d t ∂ Y 1 ∂ t 1 ) + ⋯ = ∂ Y 0 ∂ t + ε ( ∂ Y 0 ∂ t 1 + ∂ Y 1 ∂ t ) + O ( ε 2 ) , با استفاده از dt 1 / dt = ε. خواهیم داشت: d 2 y d t 2 = ∂ 2 Y 0 ∂ t 2 + ε ( 2 ∂ 2 Y 0 ∂ t ∂ t 1 + ∂ 2 Y 1 ∂ t 2 ) + O ( ε 2 ) . پس جواب های مرتبه صفر و مرتبه اول اختلالی - چند مقیاسی برای معادله دافینگ خواهد بود: ∂ 2 Y 0 ∂ t 2 + Y 0 = 0 , ∂ 2 Y 1 ∂ t 2 + Y 1 = − Y 0 3 − 2 ∂ 2 Y 0 ∂ t ∂ t 1 . راه حل برای مسئله مرتبه صفر راه حل کلی زیر وجود دارد: Y 0 ( t , t 1 ) = A ( t 1 ) e + i t + A ∗ ( t 1 ) e − i t , که A ( t 1 ) دامنه مختلط برای جواب مرتبه صفر Y 0 ( t , t 1 ) است. حال برای جواب مرتبه اول، نیرویی وابسته به زمان در سمت راست معادله دیفرانسیل دوم ظاهر می شود که برابر است با: e + i t − A 3 e + 3 i t + c . c . که در آن cc نشان دهنده مزدوج مختلط عبارت های قبلی است. از ایجاد جملات سکولار می توان با تحمیل شرط حل پذیری در دامنه A ( t 1 ) که هنوز نامشخص است جلوگیری کرد. − 3 A 2 A ∗ − 2 i d A d t 1 = 0. جواب شرط حل پذیری، همچنین شرایط اولیه y ( 0 ) = ۱ و dy/dt ( 0 ) = ۰ را برآورده می کند، یعنی: A = 1 2 exp ( 3 8 i t 1 ) . در نتیجه، جواب تقریبی با تجزیه و تحلیل چند مقیاسی عبارت است y ( t ) = cos + O ( ε ) , با استفاده از t1 = εt که تا مرتبه εt = O ( 1 ) اعتبار دارد. این با تغییرات غیرخطی فرکانس که ( وابستگی فرکانس به دامنه ) با استفاده از روش لیندستد - پوانکاره بدست می آید مطابقت دارد. این جواب تا زمان اعتبار دارد که زمان سپری شده برای سیستم از مرتبهٔ t = O ( ϵ − 2 ) باشد. جوابهای مرتبه های بالاتر - با استفاده از روش مقیاس های چندگانه - نیاز به تعریف متغییرهای مقیاسی آهستهٔ اضافی دارد، یعنی t2 = ε2 t, t3 = ε3 t و به همین ترتیب. با این حال باید توجه داشت که تعریف متغییرهای جدید می تواند ابهامات را در بسط اختلالی جواب بوجود آورد که لازم است با احتیاط با آن برخورد کرد ( به ( Kevorkian و Cole 1996 ) ؛ ( Bender و Orszag 1999 ) مراجعه کنید ) . [ ۲]

wiki: تحلیل چند مقیاسی
