در علوم کامپیوتر به خصوص در تحلیل الگوریتم ها، تحلیل سرشکنی زمان اجرای میانگین برای هر دستور را در بدترین حالت بدست می آورد. تحلیل سرشکنی با متوسط زمان اجرا تفاوت دارد چرا که زمان اجرای هر دستور در بدترین حالت را بیان می کند.
گاهی به دنبال روشی برای پیدا کردن زمان اجرای یک رویه هستیم. برای این کار، گاهی پیشنهاد می شود که به طور مستقیم بدترین زمان اجرا را بدست آوریم. این عمل باعث می شود که همیشه یک زمان اجرای خیلی زیاد بدست آید. اما تحلیل سرشکنی این امکان را به ما می دهد تا زمان اجرایی بسیار نزدیک به زمان اجرای واقعی بدست آوریم.
اینجا هدف این است که هزینه ی یک عمل را بدون توجه به ورودی به دست بیاوریم. مثلاً اگر یک شمارنده بیتی داشته باشیم، هزینه ی هر بار زیاد کردن آن برابر است با هزینه ی شمردن تا عددی که الان در شمارنده وجود دارد:
این روش ( تحلیل سرشکنی ) در واقع:
• میانگین اجرای هر عمل در بدترین حالت را بدست می آورد.
• مربوط به اجرای کل برنامه است نه دستورهای خاصی از برنامه.
• این تحلیل این گونه تفسیر می شود که بعضی از دستورهای پر هزینه در آینده برای دستورهایی که هزینه ی کمتری دارند خرج شود.
در این تحلیل از ۳ روش زیر استفاده می شود:
I. روش انبوهه[ ۲]
II. روش حسابداری[ ۳]
III. روش تابع پتانسیل[ ۴]
هر ۳ روش ذکر شده جواب درستی به ما می دهند و انتخاب استفاده از این ۳ روش بستگی به این دارد که کدام یک برای یک موقعیت خاص مناسب تر باشد.
تحلیل سرشکن شده در ابتدا از روشی به نام تحلیل متراکم پدید آمده که امروزه شامل تحلیل سر شکن است. این تکنیک بار اول توسط رابرت تارجان در مقاله پیچیدگی محاسباتی وقف شده اش در سال ۱۹۸۵ معرفی شد. که نیاز به یک شکل مفیدتر از تحلیل روشهای احتمالی متداول مورد استفاده را برطرف می کند. سرشکنی در ابتدا برای انواع خاصی از الگوریتم ها مورد استفاده قرار می گرفت، به ویژه آنهایی که مربوط به درختان باینری[ ۵] و عملیات یونیون [ ۶] هستند. با این حال، امروزه هم از این تحلیل کاربرد های زیادی دارد و هنگام تحلیل بسیاری از الگوریتم های دیگر نیز مورد استفاده قرار می گیرد.
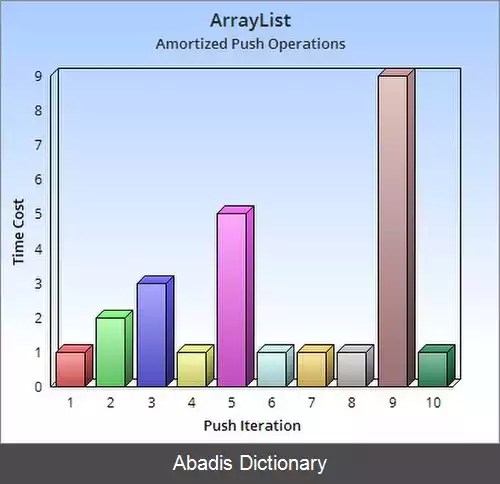
در روش انبوه[ ۲] ابتدا باید هزینه ی پی در پی اجرای n عملیات را محاسبه کنیم که در کل هزینه ی آن دنباله ای از n عملیات است و زمان اجرای آن T ( n ) است و سپس آن را بر تعداد ( n ) تقسیم کرده و در نتیجه هزینهٔ میانگین یا سرشکن شده که برابر T ( n ) / n است برای هر عمل بدست می آید. برای استفاده از این روش باید هر عمل و هزینهٔ اجرای آن را شناسایی کرد.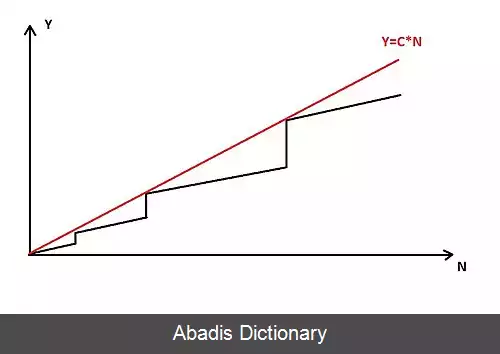


این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفگاهی به دنبال روشی برای پیدا کردن زمان اجرای یک رویه هستیم. برای این کار، گاهی پیشنهاد می شود که به طور مستقیم بدترین زمان اجرا را بدست آوریم. این عمل باعث می شود که همیشه یک زمان اجرای خیلی زیاد بدست آید. اما تحلیل سرشکنی این امکان را به ما می دهد تا زمان اجرایی بسیار نزدیک به زمان اجرای واقعی بدست آوریم.
اینجا هدف این است که هزینه ی یک عمل را بدون توجه به ورودی به دست بیاوریم. مثلاً اگر یک شمارنده بیتی داشته باشیم، هزینه ی هر بار زیاد کردن آن برابر است با هزینه ی شمردن تا عددی که الان در شمارنده وجود دارد:
این روش ( تحلیل سرشکنی ) در واقع:
• میانگین اجرای هر عمل در بدترین حالت را بدست می آورد.
• مربوط به اجرای کل برنامه است نه دستورهای خاصی از برنامه.
• این تحلیل این گونه تفسیر می شود که بعضی از دستورهای پر هزینه در آینده برای دستورهایی که هزینه ی کمتری دارند خرج شود.
در این تحلیل از ۳ روش زیر استفاده می شود:
I. روش انبوهه[ ۲]
II. روش حسابداری[ ۳]
III. روش تابع پتانسیل[ ۴]
هر ۳ روش ذکر شده جواب درستی به ما می دهند و انتخاب استفاده از این ۳ روش بستگی به این دارد که کدام یک برای یک موقعیت خاص مناسب تر باشد.
تحلیل سرشکن شده در ابتدا از روشی به نام تحلیل متراکم پدید آمده که امروزه شامل تحلیل سر شکن است. این تکنیک بار اول توسط رابرت تارجان در مقاله پیچیدگی محاسباتی وقف شده اش در سال ۱۹۸۵ معرفی شد. که نیاز به یک شکل مفیدتر از تحلیل روشهای احتمالی متداول مورد استفاده را برطرف می کند. سرشکنی در ابتدا برای انواع خاصی از الگوریتم ها مورد استفاده قرار می گرفت، به ویژه آنهایی که مربوط به درختان باینری[ ۵] و عملیات یونیون [ ۶] هستند. با این حال، امروزه هم از این تحلیل کاربرد های زیادی دارد و هنگام تحلیل بسیاری از الگوریتم های دیگر نیز مورد استفاده قرار می گیرد.
در روش انبوه[ ۲] ابتدا باید هزینه ی پی در پی اجرای n عملیات را محاسبه کنیم که در کل هزینه ی آن دنباله ای از n عملیات است و زمان اجرای آن T ( n ) است و سپس آن را بر تعداد ( n ) تقسیم کرده و در نتیجه هزینهٔ میانگین یا سرشکن شده که برابر T ( n ) / n است برای هر عمل بدست می آید. برای استفاده از این روش باید هر عمل و هزینهٔ اجرای آن را شناسایی کرد.






wiki: تحلیل سرشکنی
