اگر G یک گراف و H زیرگرافی از G باشد، منظور از یک گوش برای H در G یک مسیر با طول حداقل یک از G است که دو سر این مسیر در H قرار دارند و هیچ راس میانی آن در H قرار ندارد.
این قضیه که هاسلر ویتنی در سال ۱۹۳۲ ( میلادی ) آن را ثابت کرد شرطی لازم و کافی برای وجود تجزیه گوشی بدست می دهد و صورت آن چنین است:
G گرافی همبند و بدون راس برشی ( دوهمبند ) است، اگر و تنها اگر G تجزیه گوشی داشته باشد. بعلاوه هر دور G دور آغازینی برای یک تجزیه گوشی است. [ ۱]
اگر G گرافی همبند و بدون راس برشی باشد در این صورت گراف G ′ که حاصل زیرتقسیم یال دلخواه u v از G می باشد همچنان همبند و بدون راس برشی است. [ ۱]
بخش اگر:
بخش تنها اگر:
روش پیدا کردن تجزیه گوشی برای یک گراف ( Ear Decomposition Search ( EDS نامیده می شود که پیاده سازی های متفاوتی دارد. در یک پیاده سازی آن از یک st - شماره گذاری برای یافتن این تجزیه استفاده می شود که این روش به صورت موازی گوش ها را پیدا می کند. [ ۳] باید خاطرنشان کرد که الگوریتم های توزیعی نیز برای یافتن تجزیه گوشی به دست آمده است. [ ۴]
از تجزیه گوشی برای بهینه کردن مقایسه های داده ای استفاده می شود. [ ۵]
↑ ۱٫۰ ۱٫۱ ۱٫۲ West p. 146 ↑ West p. 147 ↑ Parallel Ear Decomposition Search ( EDS ) And ST - Numbering In Graphs ↑ A Distributed Algorithm for Ear Decomposition ↑ Ear decomposition for pair comparison data
• West, Douglas B. ( 1996 ) . Introduction to Graph Theory ( First Edition ed. ) . Prentice Hall, Inc. ISBN 0 - 13 - 227828 - 6. {{cite book}}: | edition= has extra text ( help )
• اشیاء نظریه گراف
• نظریه گراف
• نظریه میتروید
• خطاهای CS1: نوشته اضافه: ویرایش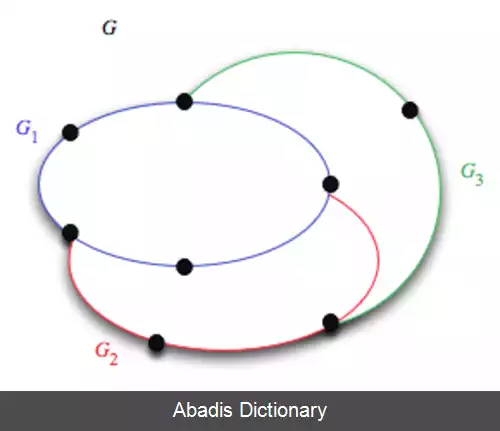
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین قضیه که هاسلر ویتنی در سال ۱۹۳۲ ( میلادی ) آن را ثابت کرد شرطی لازم و کافی برای وجود تجزیه گوشی بدست می دهد و صورت آن چنین است:
G گرافی همبند و بدون راس برشی ( دوهمبند ) است، اگر و تنها اگر G تجزیه گوشی داشته باشد. بعلاوه هر دور G دور آغازینی برای یک تجزیه گوشی است. [ ۱]
اگر G گرافی همبند و بدون راس برشی باشد در این صورت گراف G ′ که حاصل زیرتقسیم یال دلخواه u v از G می باشد همچنان همبند و بدون راس برشی است. [ ۱]
بخش اگر:
بخش تنها اگر:
روش پیدا کردن تجزیه گوشی برای یک گراف ( Ear Decomposition Search ( EDS نامیده می شود که پیاده سازی های متفاوتی دارد. در یک پیاده سازی آن از یک st - شماره گذاری برای یافتن این تجزیه استفاده می شود که این روش به صورت موازی گوش ها را پیدا می کند. [ ۳] باید خاطرنشان کرد که الگوریتم های توزیعی نیز برای یافتن تجزیه گوشی به دست آمده است. [ ۴]
از تجزیه گوشی برای بهینه کردن مقایسه های داده ای استفاده می شود. [ ۵]
↑ ۱٫۰ ۱٫۱ ۱٫۲ West p. 146 ↑ West p. 147 ↑ Parallel Ear Decomposition Search ( EDS ) And ST - Numbering In Graphs ↑ A Distributed Algorithm for Ear Decomposition ↑ Ear decomposition for pair comparison data
• West, Douglas B. ( 1996 ) . Introduction to Graph Theory ( First Edition ed. ) . Prentice Hall, Inc. ISBN 0 - 13 - 227828 - 6. {{cite book}}: | edition= has extra text ( help )
• اشیاء نظریه گراف
• نظریه گراف
• نظریه میتروید
• خطاهای CS1: نوشته اضافه: ویرایش

wiki: تجزیه گوشی
