در هندسه، تثلیث مربع نوعی مسئله قطعه بندی است که شامل بریدن یک مربع به قطعاتی است که می توان آنها را طوری کنار هم چید که سه مربع یکسان تشکیل دهند.
قطعه بندی یک مربع به سه قسمت همنهشت، یک مسئله هندسی است که قدمت آن به دوران طلایی اسلام می رسد. صنعتگری که بر هنر زلیج تسلط داشت، برای دستیابی به موزاییک های افسانه ای خود با اشکال هندسی پیچیده، به تکنیک های ابتکاری نیاز داشت. اولین راه حل برای این مشکل در قرن دهم پس از میلاد توسط ریاضیدان ایرانی ابوالوفاء بوزجانی ( ۹۴۰–۹۹۸ ) در رسالهٔ خود تحت عنوان "در مورد ساخت های هندسی لازم برای صنعتگر" ( فیما یحتاج الیه الصانع من الاعمال الهندسه ) ارائه شد. [ ۱] ابوالوفا از راه حل خود برای نشان دادن قضیه فیثاغورس نیز استفاده کرد. [ ۲] این اثبات هندسی قضیه فیثاغورس در سالهای 1835 - 1840[ ۳] توسط هنری پریگال دوباره کشف شد و در سال ۱۸۷۵ منتشر گردید[ ۴]
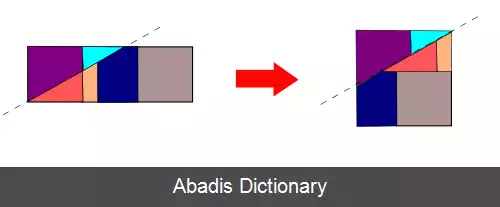
زیبایی یک قطعه بندی به پارامترهای مختلفی بستگی دارد. با این حال، جستجو برای راه حل هایی با حداقل تعداد قطعات متداول است. تثلیث مربع پیشنهاد شده توسط ابوالوفاء به دور از حداقل بودن، از ۹ قطعه استفاده می کند. در قرن چهاردهم، ابوبکر الخلیل دو راه حل ارائه داد که یکی از آنها از ۸ قطعه استفاده می کند. [ ۵] در اواخر قرن هفدهم، ژاک اوزانام به این مسئله بازگشت[ ۶] و در قرن نوزدهم، راه حل هایی با استفاده از ۸ و ۷ قطعه پیدا شد، که یکی از آنها مربوط به ریاضیدان ادوارد لوکاس بود. [ ۷] در سال ۱۸۹۱ هنری پریگال اولین راه حل شناخته شده با تنها ۶ قطعه را منتشر کرد[ ۸] ( به تصویر زیر مراجعه کنید ) . امروزه، هنوز هم قطعه بندی های جدید یافت می شوند ( به تصویر بالا مراجعه کنید ) و این حدس که ۶ حداقل تعداد قطعات لازم است هنوز ثابت نشده است.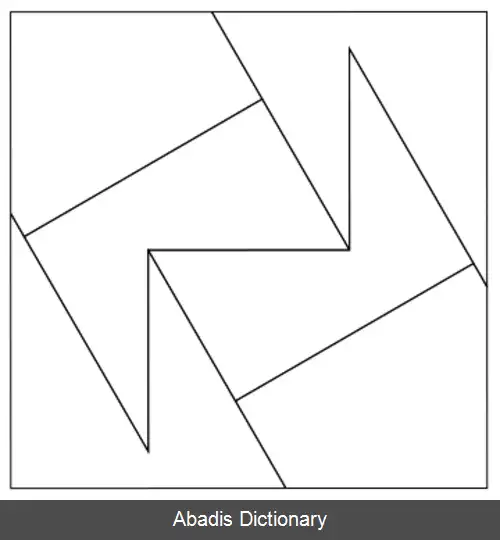
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفقطعه بندی یک مربع به سه قسمت همنهشت، یک مسئله هندسی است که قدمت آن به دوران طلایی اسلام می رسد. صنعتگری که بر هنر زلیج تسلط داشت، برای دستیابی به موزاییک های افسانه ای خود با اشکال هندسی پیچیده، به تکنیک های ابتکاری نیاز داشت. اولین راه حل برای این مشکل در قرن دهم پس از میلاد توسط ریاضیدان ایرانی ابوالوفاء بوزجانی ( ۹۴۰–۹۹۸ ) در رسالهٔ خود تحت عنوان "در مورد ساخت های هندسی لازم برای صنعتگر" ( فیما یحتاج الیه الصانع من الاعمال الهندسه ) ارائه شد. [ ۱] ابوالوفا از راه حل خود برای نشان دادن قضیه فیثاغورس نیز استفاده کرد. [ ۲] این اثبات هندسی قضیه فیثاغورس در سالهای 1835 - 1840[ ۳] توسط هنری پریگال دوباره کشف شد و در سال ۱۸۷۵ منتشر گردید[ ۴]
زیبایی یک قطعه بندی به پارامترهای مختلفی بستگی دارد. با این حال، جستجو برای راه حل هایی با حداقل تعداد قطعات متداول است. تثلیث مربع پیشنهاد شده توسط ابوالوفاء به دور از حداقل بودن، از ۹ قطعه استفاده می کند. در قرن چهاردهم، ابوبکر الخلیل دو راه حل ارائه داد که یکی از آنها از ۸ قطعه استفاده می کند. [ ۵] در اواخر قرن هفدهم، ژاک اوزانام به این مسئله بازگشت[ ۶] و در قرن نوزدهم، راه حل هایی با استفاده از ۸ و ۷ قطعه پیدا شد، که یکی از آنها مربوط به ریاضیدان ادوارد لوکاس بود. [ ۷] در سال ۱۸۹۱ هنری پریگال اولین راه حل شناخته شده با تنها ۶ قطعه را منتشر کرد[ ۸] ( به تصویر زیر مراجعه کنید ) . امروزه، هنوز هم قطعه بندی های جدید یافت می شوند ( به تصویر بالا مراجعه کنید ) و این حدس که ۶ حداقل تعداد قطعات لازم است هنوز ثابت نشده است.


wiki: تثلیث مربع
