تبدیل موجک سریع الگوریتمی ریاضی برای یافتنِ تبدیل موجک یک سیگنال است. بدین منظور تصویرِ سیگنال روی هر یک از توابع موجک در زمان ها و مقیاس های مختلف محاسبه می گردد. به عبارت دیگر، حاصل ضرب داخلی سیگنال f ( t ) با هر یک از موجک ها ϕ به شکل زیر محاسبه می شود:
s n ( J ) := 2 J ⟨ f ( t ) , ϕ ( 2 J t − n ) ⟩ ,
تصویر سیگنال بر فضای V j برابر است با:
P J ( x ) := ∑ n ∈ Z s n ( J ) ϕ ( 2 J x − n )
با داشتنِ مضارب s ( J ) با الگوریتمِ بازگشتی مضارب s ( J − 1 ) را با استفاده از رابطهٔ زیر می توان یافت:
s n ( k ) := 1 2 ∑ m = − N N a m s 2 n + m ( k + 1 )
یا:
s ( k ) ( Z ) := ( ↓ 2 ) ( a ∗ ( Z ) ⋅ s ( k + 1 ) ( Z ) )
و:
d n ( k ) := 1 2 ∑ m = − N N b m s 2 n + m ( k + 1 )
d ( k ) ( Z ) := ( ↓ 2 ) ( b ∗ ( Z ) ⋅ s ( k + 1 ) ( Z ) )
که ( ↓ 2 ) عملگر زیرنمونه گیری است و در فضای زد به صورت سری لوران ضرایب با اندیس زوج تعریف می شود:
( ↓ 2 ) ( c ( Z ) ) = ∑ k ∈ Z c 2 k Z k
بدین ترتیب:
P k ( x ) := ∑ n ∈ Z s n ( k ) ϕ ( 2 k x − n )
که حاصل جمعِ بالا برابر با تصویر سیگنال P k ( x ) بر زیرفضای V k است. در نتیجه:
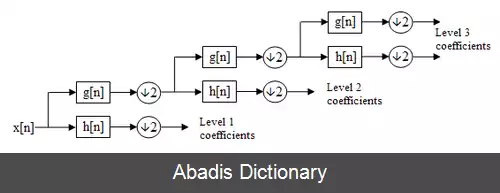
P J ( x ) = P k ( x ) + D k ( x ) + ⋯ + D J − 1 ( x )
که ضرایب جزئی برابرند با:
D k ( x ) := ∑ n ∈ Z d n ( k ) ψ ( 2 k x − n )
که ψ موجک مادر نامیده می شود.
• موجک ها
• تبدیل های گسسته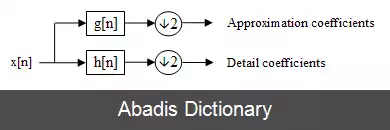
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفs n ( J ) := 2 J ⟨ f ( t ) , ϕ ( 2 J t − n ) ⟩ ,
تصویر سیگنال بر فضای V j برابر است با:
P J ( x ) := ∑ n ∈ Z s n ( J ) ϕ ( 2 J x − n )
با داشتنِ مضارب s ( J ) با الگوریتمِ بازگشتی مضارب s ( J − 1 ) را با استفاده از رابطهٔ زیر می توان یافت:
s n ( k ) := 1 2 ∑ m = − N N a m s 2 n + m ( k + 1 )
یا:
s ( k ) ( Z ) := ( ↓ 2 ) ( a ∗ ( Z ) ⋅ s ( k + 1 ) ( Z ) )
و:
d n ( k ) := 1 2 ∑ m = − N N b m s 2 n + m ( k + 1 )
d ( k ) ( Z ) := ( ↓ 2 ) ( b ∗ ( Z ) ⋅ s ( k + 1 ) ( Z ) )
که ( ↓ 2 ) عملگر زیرنمونه گیری است و در فضای زد به صورت سری لوران ضرایب با اندیس زوج تعریف می شود:
( ↓ 2 ) ( c ( Z ) ) = ∑ k ∈ Z c 2 k Z k
بدین ترتیب:
P k ( x ) := ∑ n ∈ Z s n ( k ) ϕ ( 2 k x − n )
که حاصل جمعِ بالا برابر با تصویر سیگنال P k ( x ) بر زیرفضای V k است. در نتیجه:
P J ( x ) = P k ( x ) + D k ( x ) + ⋯ + D J − 1 ( x )
که ضرایب جزئی برابرند با:
D k ( x ) := ∑ n ∈ Z d n ( k ) ψ ( 2 k x − n )
که ψ موجک مادر نامیده می شود.
• موجک ها
• تبدیل های گسسته


wiki: تبدیل موجک سریع
