تبدیل فوریه سریع

تبدیل فوریۀ سریع ( Fast Fourier transform - FFT ) نام الگوریتمی ست برای انجام تبدیلات مستقیم و معکوس فوریۀ گسسته به صورتی سریع و بسیار کارآمد. تعداد زیادی الگوریتم های تبدیل فوریه سریع مجزا وجود دارد.
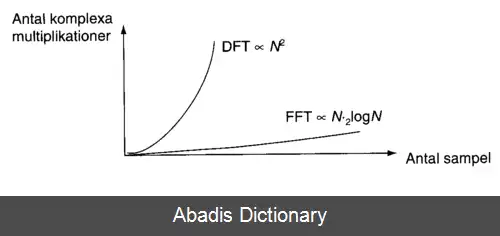
یک تبدیل فوریه سریع تجزیه یک رشته از مقادیر به مؤلفه هایی با فرکانس های متفاوت است. این عملیات در بسیاری از رشته ها مفید است ( ویژگی ها و کاربردهای تبدیل فوریه گسسته را مشاهده کنید ) اما محاسبه مستقیم آن از تعریف گاهی اوقات در عمل بسیار کند است. تبدیل فوریه سریع یک راه برای محاسبه همان نتایج به طور سریع تر است؛ محاسبه تبدیل فوریه گسسته برای n نقطه با استفاده از تعریف O ( n 2 ) عملیات ریاضی نیاز دارد در حالی که تبدیل فوریه سریع می تواند همان نتایج را در O ( n log ⁡ n ) عملیات، محاسبه نماید.
این تفاوت در سرعت می تواند بسیار چشمگیر باشد، مخصوصاً برای مجموعه داده های بزرگ. در جایی که n ممکن است در عمل هزاران یا میلیون ها باشد، زمان محاسبه در برخی موارد می تواند به اندازه چند مرتبه کاهش پیدا کند و بهبود آن در حدود n / log ⁡ n مرتبه است. این بهبود عظیم موجب شده تا بسیاری از الگوریتم های عملی تبدیل فوریه گسسته را به صورت تبدیل فوریه سریع پیاده سازی نمایند؛ بنابراین تبدیل فوریه سریع در محدوده متنوعی از کاربردها از پردازش سیگنال دیجیتال و حل معادلات دیفرانسیل با مشتقات جزئی ( پاره ای ) تا ضرب مقادیر بزرگ صحیح به کار می رود.
از تبدیل فوریه سریع به عنوان «مهم ترین الگوریتم عددی عصر زندگی ما» یاد می شود.
در طول تمامی سده گذشته و به خصوص در طی ۵۰ سال آخر آن صنایع گوناگون و رشته های مختلف دانشگاهی را می توان ذکر کرد که به واسطه اعمال ایده ها و تکنیک های گوناگون فوریه به نحو کاملی شکوفا و پررونق شده اند.
تبدیل فوریه سریع تبدیل فوریه گسسته را محاسبه می کند و دقیقاً همان نتایجی را تولید می کند که مستقیماً با تعریف تبدیل فوریه گسسته به دست می آید تنها تفاوت آن این است که بسیار سریع تر است.
اگر اعداد مختلط x۰، . . . . ، xN - 1 را در نظر بگیریم تبدیل فوریه گسسته با فرمول زیر تعریف می شود:
X k = ∑ n = 0 N − 1 x n e − i 2 π k n N k = 0 , … , N − 1.
f j = ∑ k = 0 n − 1 x k e − 2 π i n j k j = 0 , … , n − 1.