تبدیل فوریه گسسته ( Discrete Fourier Transform - DFT ) ، توابع و سیگنال های گسسته را از حوزهٔ زمان به حوزهٔ فرکانس ( و یا از حوزهٔ مکان به حوزهٔ عدد موج ) تبدیل می کند، به طوری که حاصل تبدیل نیز گسسته است. بنابراین تبدیل فوریۀ گسسته را نباید با تبدیل فوریۀ یک سیگنال گسسته، که حاصل آن پیوسته است اشتباه گرفت.
پیاده سازیِ بهینۀ تبدیلِ فوریۀ گسسته ( از نظر تعداد عملیات ریاضی لازم برای محاسبه تبدیل ) ، تبدیلِ فوریۀ سریع ( Fast Fourier Transform - FFT ) نام دارد. مهم ترین کاربرد FFT، در پردازش سیگنال است.
البته تبدیل فوریه گسسته در بررسی الگوریتم ها برای ضرب سریع چندجمله ایها نیز استفاده می شود.
X k = ∑ n = 0 N − 1 x n e − 2 π i N k n k = 0 , … , N − 1
کامل بودن تبدیل فوریه بدین معنا است که می توان سیگنال اولیه را از سیگنال انتقال یافته دوباره ساخت. به عبارت دیگر با اعمال تبدیل فوریه داده ای از دست نمی رود و تبدیل بازگشت پذیر است.
بردارهای e 2 π i N k n دو به دو برهم عمود هستند، یعنی:
∑ n = 0 N − 1 ( e 2 π i N k n ) ( e − 2 π i N k ′ n ) = N δ k k ′
که δ k k ′ تابع دلتای کرونکر می باشد.
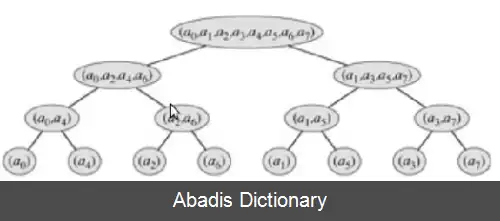
علاوه بر این کاربردها، در بررسی الگوریتم ها، برای ضرب چند جمله ای ها نیز از تبدیل فوریه سریع استفاده می شود. در این روش ابتدا چندجمله ای را به فرم دیگری تبدیل می کنیم که انجام عملیات ضرب و تقسیم بر روی این فرم نمایش می تواند سریع انجام شود. پس از انجام عملیات، با تبدیل عکس فوریه ( D F T − 1 ) می توان پاسخ را در قالب چندجمله ای بدست آورد. در ادامه به بررسی دقیق این الگوریتم می پردازیم.
برای نمایش توابع راه های گوناگونی وجود دارد، به طور مثال می توان یک تابع را با مجموعه اعضا ( برای توابع با دامنهٔ محدود ) ، ضابطهٔ کلی تابع، یک سری مانند بسط تیلور یا بسط فوریه و… نمایش داد. یک فرم که در انجام محاسبات بسیار کاراست، را در این جا توضیح می دهیم. می دانیم که در صفحه می توان هرچند جمله ای از درجه n را با دقیقاً n+1 نقطه از آن به طور یکتا مشخص کرد. مثلاً هر خط راست را می توان با دو نقطه از آن به طور یکتا مشخص کرد و برعکس؛ یا این که هر سه نقطه یک سهمی را به طور یکتا تعیین می کنند. پس یک روش نمایش چندجمله ای های درجه n، نگهداری n+1 نقطهٔ آن است. دقت کنید که این نقاط به دلخواه از دامنهٔ تابع انتخاب می شوند. به طور دقیق تر:
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفپیاده سازیِ بهینۀ تبدیلِ فوریۀ گسسته ( از نظر تعداد عملیات ریاضی لازم برای محاسبه تبدیل ) ، تبدیلِ فوریۀ سریع ( Fast Fourier Transform - FFT ) نام دارد. مهم ترین کاربرد FFT، در پردازش سیگنال است.
البته تبدیل فوریه گسسته در بررسی الگوریتم ها برای ضرب سریع چندجمله ایها نیز استفاده می شود.
X k = ∑ n = 0 N − 1 x n e − 2 π i N k n k = 0 , … , N − 1
کامل بودن تبدیل فوریه بدین معنا است که می توان سیگنال اولیه را از سیگنال انتقال یافته دوباره ساخت. به عبارت دیگر با اعمال تبدیل فوریه داده ای از دست نمی رود و تبدیل بازگشت پذیر است.
بردارهای e 2 π i N k n دو به دو برهم عمود هستند، یعنی:
∑ n = 0 N − 1 ( e 2 π i N k n ) ( e − 2 π i N k ′ n ) = N δ k k ′
که δ k k ′ تابع دلتای کرونکر می باشد.
علاوه بر این کاربردها، در بررسی الگوریتم ها، برای ضرب چند جمله ای ها نیز از تبدیل فوریه سریع استفاده می شود. در این روش ابتدا چندجمله ای را به فرم دیگری تبدیل می کنیم که انجام عملیات ضرب و تقسیم بر روی این فرم نمایش می تواند سریع انجام شود. پس از انجام عملیات، با تبدیل عکس فوریه ( D F T − 1 ) می توان پاسخ را در قالب چندجمله ای بدست آورد. در ادامه به بررسی دقیق این الگوریتم می پردازیم.
برای نمایش توابع راه های گوناگونی وجود دارد، به طور مثال می توان یک تابع را با مجموعه اعضا ( برای توابع با دامنهٔ محدود ) ، ضابطهٔ کلی تابع، یک سری مانند بسط تیلور یا بسط فوریه و… نمایش داد. یک فرم که در انجام محاسبات بسیار کاراست، را در این جا توضیح می دهیم. می دانیم که در صفحه می توان هرچند جمله ای از درجه n را با دقیقاً n+1 نقطه از آن به طور یکتا مشخص کرد. مثلاً هر خط راست را می توان با دو نقطه از آن به طور یکتا مشخص کرد و برعکس؛ یا این که هر سه نقطه یک سهمی را به طور یکتا تعیین می کنند. پس یک روش نمایش چندجمله ای های درجه n، نگهداری n+1 نقطهٔ آن است. دقت کنید که این نقاط به دلخواه از دامنهٔ تابع انتخاب می شوند. به طور دقیق تر:


wiki: تبدیل فوریه گسسته
