در پردازش کوانتومی، تبدیل فوریه کوانتومی یک نگاشت خطی روی کیوبیت ها است و مشابه کوانتومی تبدیل فوریه گسسته می باشد. تبدیل فوریه کوانتومی جزئی از بسیاری از الگوریتم های کوانتومی است، و به خصوص در الگوریتم شور برای فاکتورگیری و محاسبهٔ لگاریتم گسسته، الگوریتم تخمین فاز کوانتومی برای تخمین ویژه مقدارهای یک عملگر یکانی و الگوریتم زیرگروه پنهان کاربرد دارد.
تبدیل فوریه کوانتومی با بازدهی ( efficiency ) بالایی بر روی یک رایانه کوانتومی قابل پیاده سازی است. تا به امروز، بهترین الگوریتم های یافته شده برای تبدیل فوریه کوانتومی نیاز به O ( n log n ) گیت برای دست یابی به یک تقریب کارا دارند. [ ۱]
تبدیل فوریه کوانتومی همان تبدیل فوریه گسسته کلاسیک است که به بردار دامنه های یک حالت کوانتومی اعمال شده است. تبدیل فوریه کلاسیک گسسته روی یک بردار در C N مانند ( x0, … , xN−1 ) عمل می کند و طبق رابطهٔ زیر آن را به ( y0, … , yN−1 ) می برد:
که ω = e 2 π i N ریشه های واحد هستند.
به طور مشابه ٬تبدیل فوریه کوانتومی، بر روی حالت کوانتومیِ ∑ i = 0 N − 1 x i | i ⟩ عمل می کند و طبق رابطهٔ زیر آن را به ∑ i = 0 N − 1 y i | i ⟩ می برد:
y k = 1 N ∑ j = 0 N − 1 x j ω j k .
این رابطه را به صورت نگاشت زیر نیز می توان نشان داد:
به طور هم ارز ٬تبدیل فوریه کوانتومی، را می توان به عنوان یک ماتریس یکانی که بر روی بردار حالت های کوانتومی عمل می کند نشان داد. این ماتریس ( F N ) چنین خواهد بود:
بیشتر خواص تبدیل فوریه کوانتومی از اینکه این تبدیل یک تبدیل یکانی ( unitary transformation ) است نتیجه می شوند. این مسئله را می توان با انجام ضرب ماتریسی F F † = F † F = I تحقیق کرد. به طور هم ارز می شود نشان داد که بردارهای با نرم ۱ به برداری با نرم ۱ نگاشته می شوند.
از ویژگی یکانی نتیجه می شود که معکوس تبدیل فوریه کوانتومی Hermitian adjoint ماتریس فوریه است، یعنی F − 1 = F † . از آنجایی که یک مدار کوانتومی efficient برای تبدیل فوریه کوانتومی قابل پیاده سازی است، مدار می تواند به طور عکس برای انجام معکوس تبدیل فوریه کوانتومی به کار رود. هر دوی این تبدیل ها به طور efficient روی یک رایانه کوانتومی قابل پیاده سازی هستند.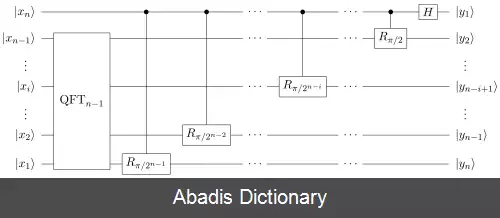
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتبدیل فوریه کوانتومی با بازدهی ( efficiency ) بالایی بر روی یک رایانه کوانتومی قابل پیاده سازی است. تا به امروز، بهترین الگوریتم های یافته شده برای تبدیل فوریه کوانتومی نیاز به O ( n log n ) گیت برای دست یابی به یک تقریب کارا دارند. [ ۱]
تبدیل فوریه کوانتومی همان تبدیل فوریه گسسته کلاسیک است که به بردار دامنه های یک حالت کوانتومی اعمال شده است. تبدیل فوریه کلاسیک گسسته روی یک بردار در C N مانند ( x0, … , xN−1 ) عمل می کند و طبق رابطهٔ زیر آن را به ( y0, … , yN−1 ) می برد:
که ω = e 2 π i N ریشه های واحد هستند.
به طور مشابه ٬تبدیل فوریه کوانتومی، بر روی حالت کوانتومیِ ∑ i = 0 N − 1 x i | i ⟩ عمل می کند و طبق رابطهٔ زیر آن را به ∑ i = 0 N − 1 y i | i ⟩ می برد:
y k = 1 N ∑ j = 0 N − 1 x j ω j k .
این رابطه را به صورت نگاشت زیر نیز می توان نشان داد:
به طور هم ارز ٬تبدیل فوریه کوانتومی، را می توان به عنوان یک ماتریس یکانی که بر روی بردار حالت های کوانتومی عمل می کند نشان داد. این ماتریس ( F N ) چنین خواهد بود:
بیشتر خواص تبدیل فوریه کوانتومی از اینکه این تبدیل یک تبدیل یکانی ( unitary transformation ) است نتیجه می شوند. این مسئله را می توان با انجام ضرب ماتریسی F F † = F † F = I تحقیق کرد. به طور هم ارز می شود نشان داد که بردارهای با نرم ۱ به برداری با نرم ۱ نگاشته می شوند.
از ویژگی یکانی نتیجه می شود که معکوس تبدیل فوریه کوانتومی Hermitian adjoint ماتریس فوریه است، یعنی F − 1 = F † . از آنجایی که یک مدار کوانتومی efficient برای تبدیل فوریه کوانتومی قابل پیاده سازی است، مدار می تواند به طور عکس برای انجام معکوس تبدیل فوریه کوانتومی به کار رود. هر دوی این تبدیل ها به طور efficient روی یک رایانه کوانتومی قابل پیاده سازی هستند.

wiki: تبدیل فوریه کوانتومی
