تانسور تنش ماکسول

تانسور تنش ماکسول ( نام گذاری شده پس از جیمز کلارک ماکسول ) یک تانسور مرتبهٔ دوم است که در الکترومغناطیس کلاسیک برای نمایش چگونگی برهم کنش نیروهای الکترومغناطیسی با تکانه مکانیکی استفاده می شود. در شرایط ساده٬ مانند نیروی وارد بر یک بار نقطه ای در حال حرکت آزاد در میدان مغناطیسی همگن می توان نیروی وارد شده بر بار را از قانون نیروی لورنتز یافت. در شرایط پیچیده تر، به دست آوردن این نیرو به روش قبل بسیار دشوارتر یا غیرممکن می شود. از این رو بهتر است رابطهٔ بین میدان های الکتریکی و تکانهٔ الکترومغناطیسی با تکانهٔ مکانیکی را مستقیماً از معادلات ماکسول بیابیم و با استفاده از تانسورها به صورت فشرده بیان کنیم.
با استفاده از معادلات ماکسول و قانون نیروی لورنتز، به یک رابطه برای نیروی در واحد حجم وارد بر یک توزیع بار دلخواه می رسیم، که معادلهٔ نسبتاً پیچیده ای است. با معرفی تانسور تنش ماکسول به صورتی که در زیر می آید هم معادلات به صورت زیباتری نوشته می شوند و هم به رابطه ای مشابه رابطهٔ پایستگی انرژی در الکترومغناطیس، برای تکانه می ٰرسیم و مفهوم تکانهٔ ذخیره شده در میدان ها را معرفی می کنیم.
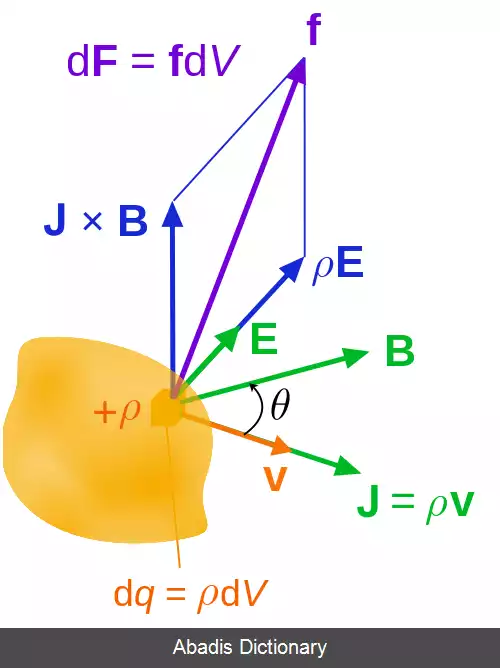
۱. از قانون لورنتز، نیروی در واحد حجم برای یک توزیع بار دلخواه چنین است:
۲. حال از معادلات ماکسول در بالا٬ توزیع های چشمه ( جریان و بار ) را با میدان ها جایگزین می کنیم:
۳. با استفاده از رابطه
می توان نیرو را چنین بازنویسی کرد:
۴. با مقایسه قسمت اول ( شامل E ) با قسمت دوم ( شامل B ) ، یک جمله در قسمت دوم گمشده به نظر می رسد که با استفاده از معادلات ماکسول ( رابطهٔ دوم در جدول بالا ) در نتیجه، با افزودن B ) B•∇ ) قابل جبران سازی است. با استفاده از اتحاد برداری
1 2 ∇ ( A ⋅ A ) = A × ( ∇ × A ) + ( A ⋅ ∇ ) A
می شود معادله نیرو را چنین نوشت:
f = ϵ 0 + 1 μ 0 − 1 2 ∇ ( ϵ 0 E 2 + 1 μ 0 B 2 ) − ϵ 0 ∂ ∂ t ( E × B )
این معادله، معادلهٔ نهایی برای نیروی الکترومغناطیسی و دربرگیرندهٔ همهٔ جنبه های فیزیکی مسئله است، اما می توان این معادله را به صورت بسیار فشرده تر و زیباتر با استفاده از تانسورها نمایش داد. تانسور تنش ماکسول را چنین معرفی می کنیم:
σ i j ≡ ϵ 0 ( E i E j − 1 2 δ i j E 2 ) + 1 μ 0 ( B i B j − 1 2 δ i j B 2 )