نمونه های ابتدایی مثلثات را در هزاره دوم پیش از میلاد در مصر و بابل میتوان مشاهده کرد. در یونان باستان از رابطه بین یک وتر دایره با زاویه مربوط به آن استفاده میگشت که همچنان روش ابتدایی بود. ستاره شناسان هندی نیز مثلثات را به کار می گرفتند. در دوره گوپتا، افرادی مانند آریابهاتا ( سده شش پیش از میلاد ) از مثلثات استفاده کردند.
در قرون وسطا، دانشمندان مسلمان خواجه نصیرالدین طوسی ابوریحان بیرونی خوارزمی و مروزی در تکمیل آن کوشیدند تا در نهایت فرمولهای مثلثاتی امروزی را بتانی در قرن دهم میلادی ارائه داد.
افرادی چون رگیومونتانوس، مثلثات مسلمین را به لاتین ترجمه کردند و به اروپا بردند. توسعه مثلثات نوین، در عصر روشنگری توسط دانشمندانی چون آیزاک نیوتن و جیمز استرلینگ آغاز شد و لئونارد اویلر، ما را به امروز رساند.
نام گذاری مثلثات در علوم اسلامی، به دلیل آن است که پایه این علم، مثلث است. که در ترجمه اروپایی هم بطور تحت اللفظی وارد شده است ترایگون=سه ضلعی .
نام سینوس از واژه سانسکریت جیوا گرفته شده است. این واژه در عربی، به جیب تبدیل شد و پس از ترجمه متون عربی به لاتین، مترجمان که آن را به اشتباه، جَیب ( به معنی خلیج ) خوانده بودند، این واژه را به سینوس ( به معنی خلیج ) برگرداندند. [ ۱]
ریاضیات باستانی مصر و بابل، قضیه هایی را در زمینه نسبت میان اضلاع مثلث های مشابه می دانستند. البته از آن جایی که مفهوم زاویه را نمی دانستند، به جای آن، محدود به مطالعه اضلاع مثلث بودند. [ ۲]
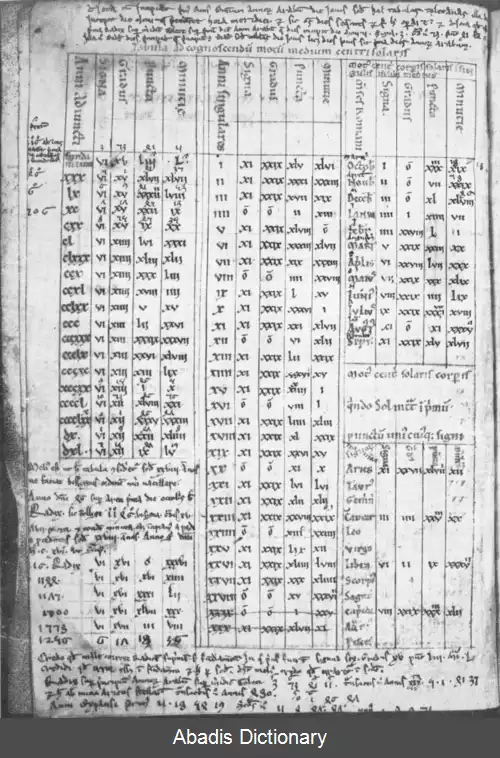
ستاره شناسان بابلی، جزئیات اندازه گیری طلوع و غروب ستاره ها، حرکت سیارات و کسوف و خسوف را ثبت می کردند. برای همه این موارد، آشنایی با اندازه گیری زاویه ها ضروری بود. [ ۳] برخی معتقدند که بابلیان جدول سکانت ها را هم تهیه کرده بودند. [ ۴] البته مشخص نیست که این جدول، مربوط به مثلث های فیثاغورسی، حل معادلات درجه دوم یا جدول مثلثاتی بوده است.
مصریان شکل اولیه ای از مثلثات را برای ساختن اهرام در هزاره دوم پیش از میلاد به کار می بردند. [ ۳]
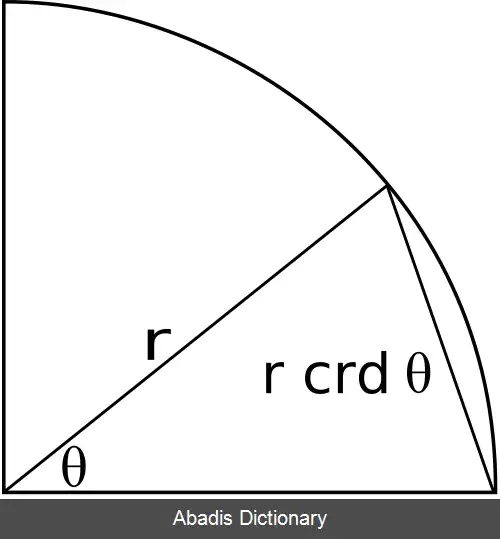
ریاضی دانان یونان باستان، از وتر پاره خطی در دایره و روبروی یک زاویه مرکزی استفاده میکردند. نصف وتر، برابر سینوس نصف زاویه مرکزی روبروی آن است:
و در نتیجه، تابع سینوس به عنوان نصف وتر، شناخته می شد. به دلیل این رابطه، تعدادی از اتحادهای مثلثاتی کنونی برای ریاضی دانان یونان باستان، البته در شکل دیگری شناخته شده بودند. [ ۵]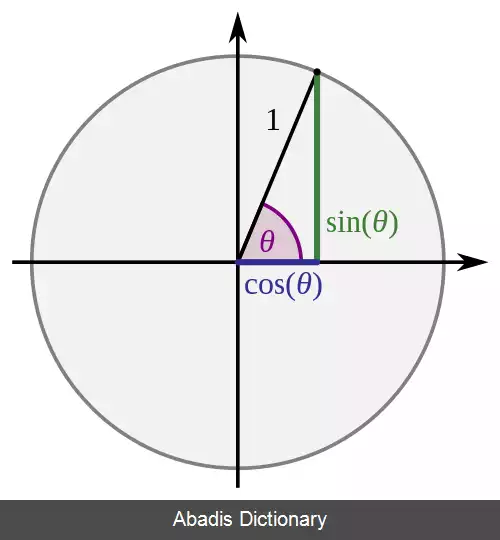

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر قرون وسطا، دانشمندان مسلمان خواجه نصیرالدین طوسی ابوریحان بیرونی خوارزمی و مروزی در تکمیل آن کوشیدند تا در نهایت فرمولهای مثلثاتی امروزی را بتانی در قرن دهم میلادی ارائه داد.
افرادی چون رگیومونتانوس، مثلثات مسلمین را به لاتین ترجمه کردند و به اروپا بردند. توسعه مثلثات نوین، در عصر روشنگری توسط دانشمندانی چون آیزاک نیوتن و جیمز استرلینگ آغاز شد و لئونارد اویلر، ما را به امروز رساند.
نام گذاری مثلثات در علوم اسلامی، به دلیل آن است که پایه این علم، مثلث است. که در ترجمه اروپایی هم بطور تحت اللفظی وارد شده است ترایگون=سه ضلعی .
نام سینوس از واژه سانسکریت جیوا گرفته شده است. این واژه در عربی، به جیب تبدیل شد و پس از ترجمه متون عربی به لاتین، مترجمان که آن را به اشتباه، جَیب ( به معنی خلیج ) خوانده بودند، این واژه را به سینوس ( به معنی خلیج ) برگرداندند. [ ۱]
ریاضیات باستانی مصر و بابل، قضیه هایی را در زمینه نسبت میان اضلاع مثلث های مشابه می دانستند. البته از آن جایی که مفهوم زاویه را نمی دانستند، به جای آن، محدود به مطالعه اضلاع مثلث بودند. [ ۲]
ستاره شناسان بابلی، جزئیات اندازه گیری طلوع و غروب ستاره ها، حرکت سیارات و کسوف و خسوف را ثبت می کردند. برای همه این موارد، آشنایی با اندازه گیری زاویه ها ضروری بود. [ ۳] برخی معتقدند که بابلیان جدول سکانت ها را هم تهیه کرده بودند. [ ۴] البته مشخص نیست که این جدول، مربوط به مثلث های فیثاغورسی، حل معادلات درجه دوم یا جدول مثلثاتی بوده است.
مصریان شکل اولیه ای از مثلثات را برای ساختن اهرام در هزاره دوم پیش از میلاد به کار می بردند. [ ۳]
ریاضی دانان یونان باستان، از وتر پاره خطی در دایره و روبروی یک زاویه مرکزی استفاده میکردند. نصف وتر، برابر سینوس نصف زاویه مرکزی روبروی آن است:
و در نتیجه، تابع سینوس به عنوان نصف وتر، شناخته می شد. به دلیل این رابطه، تعدادی از اتحادهای مثلثاتی کنونی برای ریاضی دانان یونان باستان، البته در شکل دیگری شناخته شده بودند. [ ۵]






wiki: تاریخ مثلثات
