در ریاضیات تابع یکنوا[ ۱] [ ۲] تابعی است بین مجموعه های مرتب که یا ترتیب را حفظ می کند یا برعکس می کند. این مفهوم برای اولین بار در در حساب دیفرانسیل و انتگرال مطرح شد و بعدها به نظریه انتزاعی تر نظریه ترتیب تعمیم یافت.
در حساب دیفرانسیل و انتگرال، تابع f روی زیرمجموعه ای از اعداد حقیقی یکنوا گفته می شود اگر و تنها اگر کاملاً غیر صعودی یا کاملاً غیرنزولی باشد.
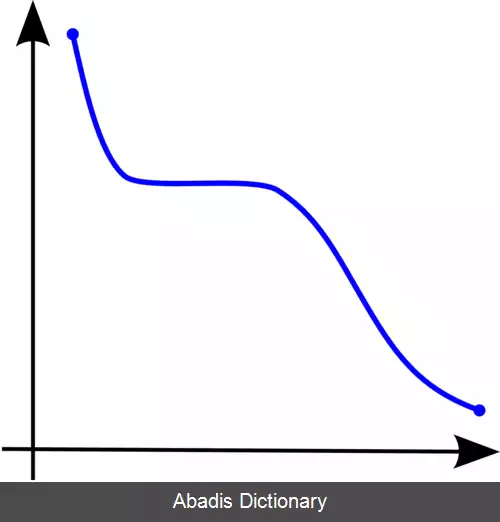
یک تابع یکنوای صعودی است ( یا صعودی یا غیر نزولی ) ، اگر برای همه x و y که x ≤ y آنگاه f ( x ) ≤ f ( y ) و بنابراین f ترتیب را حفظ می کند ( نگاه کنید به شکل ۲ ) . به همین ترتیب یک تابع یکنوای نزولی ( یا نزولی یا غیرصعودی ) است اگر برای x ≤ y داشته باشیم f ( x ) ≥ f ( y ) که در این صورت تابع ترتیب را معکوس می کند ( نگاه کنید به شکل ۱ ) اگر ≤ در تعریف یکنوایی با < جایگزین شود، آنگاه شرط قوی تری حاصل می شود. تابعی با این خاصیت صعودی اکیداً صعودی خوانده می شود. همچنین مفهوم اکیداً نزولی نیز وجود دارد. توابع اکیداً صعودی یا اکیداً نزولی یک به یک نیز هستند.
خواص زیر برای تابع یکنوا f : R → R برقرار هستند:
• f {\displaystyle f} دارای حد راست و چپ است.
• f {\displaystyle f} در مثبت بینهایت و منفی بینهایت ( ± ∞ {\displaystyle \pm \infty } ) دارای حد است که این حد یا یک عدد حقیقی است یا ∞ {\displaystyle \infty } یا ( − ∞ ) {\displaystyle \left ( - \infty \right ) }
• f {\displaystyle f} تنها می تواند پرش ناپیوستگی داشته باشد.
• f {\displaystyle f} تنها می تواند تعداد شمارایی ناپیوستگی در دامنه اش داشته باشد.
این خواص دلیل مفید بودن توابع یکنوا در آنالیز ریاضی هستند. دو واقعیت دربارهٔ این توابع عبارتند از:
• اگر f {\displaystyle f} یک تابع یکنوا باشد که روی بازه I {\displaystyle I} تعریف شده باشد، آنگاه f {\displaystyle f} تقریباً در همه جا روی I {\displaystyle I} قابل مشتق گیری است. به عبارت دیگر برای مجموعه { x : x ∈ I } {\displaystyle \left\{x:x\in I\right\}} از اعداد x {\displaystyle x} در I {\displaystyle I} که f {\displaystyle f} در نقطه x {\displaystyle x} قابل مشتق گیری نباشد، اندازه لبک صفر دارد.
• اگر f {\displaystyle f} تابعی یکنوا باشد که روی بازه {\displaystyle \left} تعریف شده است آنگاه f {\displaystyle f} انتگرال ریمان دارد.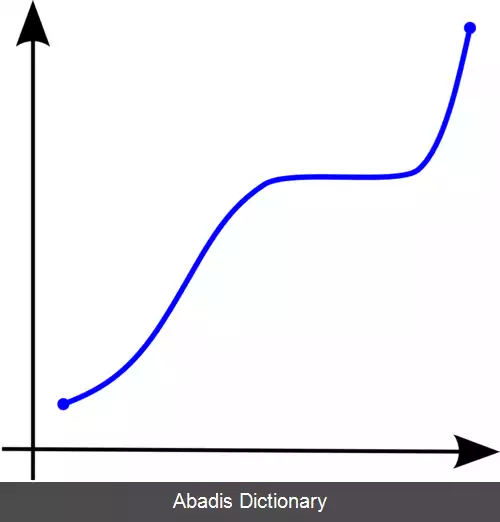
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر حساب دیفرانسیل و انتگرال، تابع f روی زیرمجموعه ای از اعداد حقیقی یکنوا گفته می شود اگر و تنها اگر کاملاً غیر صعودی یا کاملاً غیرنزولی باشد.
یک تابع یکنوای صعودی است ( یا صعودی یا غیر نزولی ) ، اگر برای همه x و y که x ≤ y آنگاه f ( x ) ≤ f ( y ) و بنابراین f ترتیب را حفظ می کند ( نگاه کنید به شکل ۲ ) . به همین ترتیب یک تابع یکنوای نزولی ( یا نزولی یا غیرصعودی ) است اگر برای x ≤ y داشته باشیم f ( x ) ≥ f ( y ) که در این صورت تابع ترتیب را معکوس می کند ( نگاه کنید به شکل ۱ ) اگر ≤ در تعریف یکنوایی با < جایگزین شود، آنگاه شرط قوی تری حاصل می شود. تابعی با این خاصیت صعودی اکیداً صعودی خوانده می شود. همچنین مفهوم اکیداً نزولی نیز وجود دارد. توابع اکیداً صعودی یا اکیداً نزولی یک به یک نیز هستند.
خواص زیر برای تابع یکنوا f : R → R برقرار هستند:
• f {\displaystyle f} دارای حد راست و چپ است.
• f {\displaystyle f} در مثبت بینهایت و منفی بینهایت ( ± ∞ {\displaystyle \pm \infty } ) دارای حد است که این حد یا یک عدد حقیقی است یا ∞ {\displaystyle \infty } یا ( − ∞ ) {\displaystyle \left ( - \infty \right ) }
• f {\displaystyle f} تنها می تواند پرش ناپیوستگی داشته باشد.
• f {\displaystyle f} تنها می تواند تعداد شمارایی ناپیوستگی در دامنه اش داشته باشد.
این خواص دلیل مفید بودن توابع یکنوا در آنالیز ریاضی هستند. دو واقعیت دربارهٔ این توابع عبارتند از:
• اگر f {\displaystyle f} یک تابع یکنوا باشد که روی بازه I {\displaystyle I} تعریف شده باشد، آنگاه f {\displaystyle f} تقریباً در همه جا روی I {\displaystyle I} قابل مشتق گیری است. به عبارت دیگر برای مجموعه { x : x ∈ I } {\displaystyle \left\{x:x\in I\right\}} از اعداد x {\displaystyle x} در I {\displaystyle I} که f {\displaystyle f} در نقطه x {\displaystyle x} قابل مشتق گیری نباشد، اندازه لبک صفر دارد.
• اگر f {\displaystyle f} تابعی یکنوا باشد که روی بازه {\displaystyle \left} تعریف شده است آنگاه f {\displaystyle f} انتگرال ریمان دارد.



wiki: تابع یکنوا
