تابع گرین به انگلیسی ( Green's function ) مفهومی است که اولین بار در دهه 1830 توسط جرج گرین ریاضی دان انگلیسی مطرح شد. به طور کلی تابع گرین هسته انتگرال است که برای حل معادلات دیفرانسیل از جمله معادلات دیفرانسیل معمولی با شرایط اولیه یا مرزی و هم چنین مسائل دشوارتر مانند معادلات دیفرانسیل با مشتقات جزئی غیرهمگن با شرایط مرزی مورد استفاده قرار میگیرد. به طور دقیق فرض کنید عملگر دیفرانسیلی خطیL=L ( x ) که روی مجموعه ای از توزیع ها روی D ⊆ R n عمل میکند داده شده است. یک تابع گرین در نقطه s ∈ Dمتناظر با عملگر L ، هر جواب معادله زیر است:
L G ( x , s ) = δ ( x − s )
که δ تابع دلتای دیراک است. در واقع G تابعی است که با اثر کردن عملگر دیفرانسیلی L روی آن تابع دلتای دیراک حاصل می شود. با ضرب طرفین این رابطه در f ( s ) و انتگرال گیری خواهیم داشت:
∫ L G ( x , s ) f ( s ) d s = ∫ δ ( x − s ) f ( s ) d s
با استفاده از خواص تابع دلتای دیراک میدانیم عبارت سمت راست رابطه فوق برابر f ( x ) است، از طرفی چون عملگر L خطی است و فقط روی x اثر میکند عبارت سمت چپ رابطه فوق را میتوانیم به صورت زیر بنویسیم:
L = ( ∫ G ( x , s ) f ( s ) d s )
این روند برای حل معادلات دیفرانسیل زیر که u=u ( x ) بسیار مفید است:
L u ( x ) = f ( x ) ⇒ L u ( x ) = L ( ∫ G ( x , s ) f ( s ) d x )
u ( x ) = ∫ G ( x , s ) f ( s ) d s
• شرط پیوستگی
تابع گرین مسئله اشتورم - لیوویل هموار پیوسته است یعنی:
x = s − x = s + = 0 ⇒ G ( x , s − ) = G ( x , s + )
• شرط پرش:
x = s − x = s + = 1 p ( s )
به کمک این خواص میتوان تابع گرین مربوط به یک مسئله اشتورم - لیوویل هموار را مشخص کرد.
اگر در بعد دو و سه دامنه مورد نظر ناحیه D باشد آنگاه شرایط مرزی روی مرز D یعنی ∂ D تعریف میشود. فرض میکنیم D کراندار باشد:
مشابه قسمت یک بعدی میتوانیم تابع گرین دو بعدی را نیز به صورت زیر تعریف کنیم:
∇ 2 G ( x , s ) = δ ( x − s )
با شرایط مرزی
a G ( x , s ) + b n . ∇ x G ( x , s ) = 0
که ∇ تابع گرادیان است.
برای تعیین تابع گرین ، گرادیان را حول نقاطی بررسی میکنیم که به s نزدیک اند: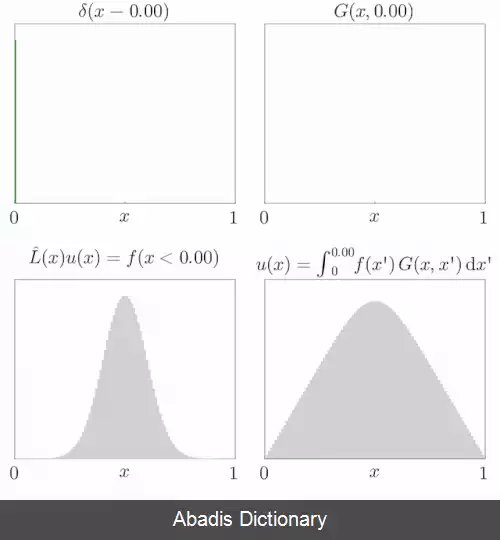
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفL G ( x , s ) = δ ( x − s )
که δ تابع دلتای دیراک است. در واقع G تابعی است که با اثر کردن عملگر دیفرانسیلی L روی آن تابع دلتای دیراک حاصل می شود. با ضرب طرفین این رابطه در f ( s ) و انتگرال گیری خواهیم داشت:
∫ L G ( x , s ) f ( s ) d s = ∫ δ ( x − s ) f ( s ) d s
با استفاده از خواص تابع دلتای دیراک میدانیم عبارت سمت راست رابطه فوق برابر f ( x ) است، از طرفی چون عملگر L خطی است و فقط روی x اثر میکند عبارت سمت چپ رابطه فوق را میتوانیم به صورت زیر بنویسیم:
L = ( ∫ G ( x , s ) f ( s ) d s )
این روند برای حل معادلات دیفرانسیل زیر که u=u ( x ) بسیار مفید است:
L u ( x ) = f ( x ) ⇒ L u ( x ) = L ( ∫ G ( x , s ) f ( s ) d x )
u ( x ) = ∫ G ( x , s ) f ( s ) d s
• شرط پیوستگی
تابع گرین مسئله اشتورم - لیوویل هموار پیوسته است یعنی:
x = s − x = s + = 0 ⇒ G ( x , s − ) = G ( x , s + )
• شرط پرش:
x = s − x = s + = 1 p ( s )
به کمک این خواص میتوان تابع گرین مربوط به یک مسئله اشتورم - لیوویل هموار را مشخص کرد.
اگر در بعد دو و سه دامنه مورد نظر ناحیه D باشد آنگاه شرایط مرزی روی مرز D یعنی ∂ D تعریف میشود. فرض میکنیم D کراندار باشد:
مشابه قسمت یک بعدی میتوانیم تابع گرین دو بعدی را نیز به صورت زیر تعریف کنیم:
∇ 2 G ( x , s ) = δ ( x − s )
با شرایط مرزی
a G ( x , s ) + b n . ∇ x G ( x , s ) = 0
که ∇ تابع گرادیان است.
برای تعیین تابع گرین ، گرادیان را حول نقاطی بررسی میکنیم که به s نزدیک اند:

wiki: تابع گرین
