در ریاضیات، تابع چبیشف توسط پافنوتی چبیشف تعریف شد. تابع چبیشف به دو شکل مطرح است.
تابع اولیهٔ چبیشف را با علامت ϑ یا θ نشان می دهند و به شکل زیر تعریف می شود.
ϑ ( x ) = ∑ p ≤ x ln p
برای مثال
ϑ ( 20 ) = l n ( 2 ) + l n ( 3 ) + l n ( 5 ) + l n ( 7 ) + l n ( 11 ) + l n ( 13 ) + l n ( 17 ) + l n ( 19 ) = 16. 08. . . .
تابع ثانویه چبیشف را با علامت ψ نشان می دهند و به شکل زیر تعریف می شود.
ψ ( x ) = ∑ p k ≤ x log p
ψ ( 20 ) = l n ( 2 ) + l n ( 3 ) + l n ( 2 ) + l n ( 5 ) + l n ( 7 ) + l n ( 2 ) + l n ( 3 ) + l n ( 11 ) + l n ( 13 ) + l n ( 2 ) + l n ( 17 ) + l n ( 19 ) = 19. 26. . .
ψ ( x ) = ∑ p k ≤ x log p = ∑ n ≤ x Λ ( n ) = ∑ p ≤ x ⌊ log p x ⌋ log p ,
در این جا، Λ ( n ) تابع منگولد است.
ψ ( x ) = ∑ p ≤ x k log p
ϑ ( x ) = ∑ p ≤ x log p = log ∏ p ≤ x p = log ( x # ) .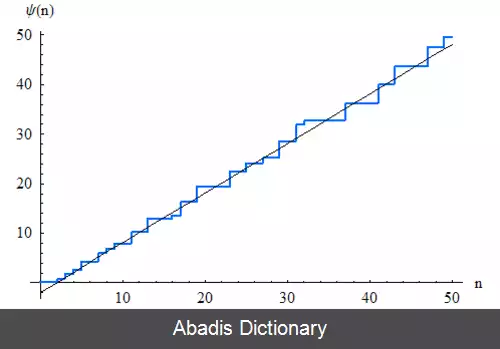
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتابع اولیهٔ چبیشف را با علامت ϑ یا θ نشان می دهند و به شکل زیر تعریف می شود.
ϑ ( x ) = ∑ p ≤ x ln p
برای مثال
ϑ ( 20 ) = l n ( 2 ) + l n ( 3 ) + l n ( 5 ) + l n ( 7 ) + l n ( 11 ) + l n ( 13 ) + l n ( 17 ) + l n ( 19 ) = 16. 08. . . .
تابع ثانویه چبیشف را با علامت ψ نشان می دهند و به شکل زیر تعریف می شود.
ψ ( x ) = ∑ p k ≤ x log p
ψ ( 20 ) = l n ( 2 ) + l n ( 3 ) + l n ( 2 ) + l n ( 5 ) + l n ( 7 ) + l n ( 2 ) + l n ( 3 ) + l n ( 11 ) + l n ( 13 ) + l n ( 2 ) + l n ( 17 ) + l n ( 19 ) = 19. 26. . .
ψ ( x ) = ∑ p k ≤ x log p = ∑ n ≤ x Λ ( n ) = ∑ p ≤ x ⌊ log p x ⌋ log p ,
در این جا، Λ ( n ) تابع منگولد است.
ψ ( x ) = ∑ p ≤ x k log p
ϑ ( x ) = ∑ p ≤ x log p = log ∏ p ≤ x p = log ( x # ) .

wiki: تابع چبیشف
