در ریاضیات تابع f : X → Y را پوشا ( به انگلیسی: Surjective ) می نامیم، هرگاه هر عضو مانند y ∈ Y با یک عضو مانند x ∈ X متناظر شده باشد، به گونه ای که f ( x ) = y . تابع f ممکن است بیشتر از یک عضو از X را به یک عضو خاص از Y تصویر کند.
واژهٔ پوشا و واژه های مرتبط یک به یک و دوسویی توسط نیکلا بورباکی، تخلص گروهی از ریاضی دانان اساساً فرانسوی قرن بیستمی که کتاب های متعددی در مورد توضیح ریاضیات پیشرفته مدرن نوشتند، در سال ۱۹۳۵ معرفی شدند. واژهٔ پوشا به این معنی است که تصویر دامنهٔ تابع کاملاً برد تابع را می پوشاند.
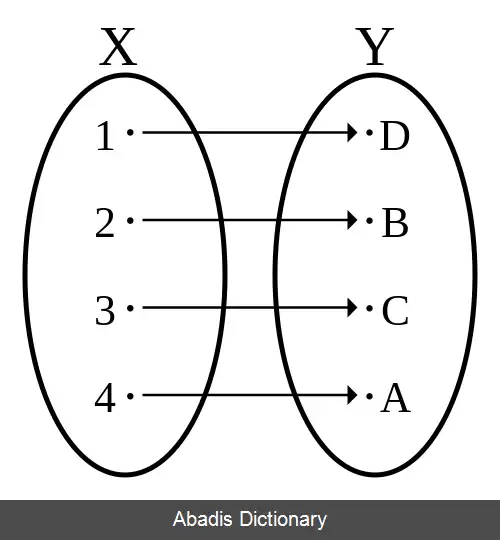
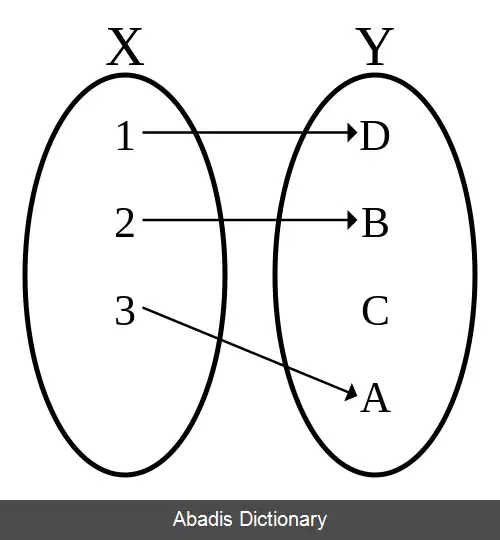
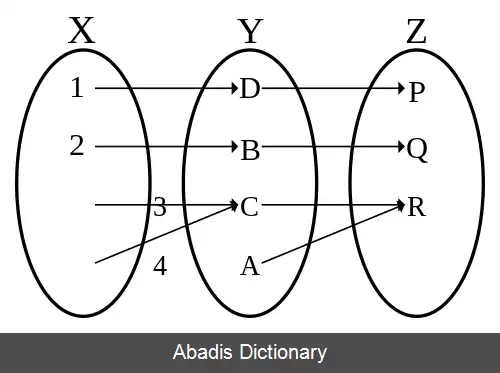
تابع پوشا تابعی است که تصویر آن برابر بردش می باشد. یا به طور معادل تابع f با دامنهٔ و برد پوشا است اگر به ازای هر y ∈ Y وجود داشته باشد حداقل یک x ∈ X که . توابع پوشا برخی اوقات با یک پیکان راست پیما دو سر نمایش داده می شوند، مانند f: X ↠ Y.
f : X → Y ، آنگاه f پوشا است اگر
∀ y ∈ Y ; ∃ x ∈ X ; f ( x ) = y . [ ۱]
به ازای هر مجموعهٔ تابع همانی بر روی پوشا است.
تابع f : Z → { 0 , 1 } با ضابطهٔ f ( n ) = n mod 2 ( تابعی که اعداد زوج را به صفر و اعداد فرد را به یک تصویر می کند ) تابعی پوشا است.
تابع f : R → R با ضابطهٔ f ( x ) = 2 x + 1 پوشا ( و حتی دو سویی ) است، چون به ازای هر عدد حقیقی x = ( y − 1 ) / 2 ای وجود دارد به گونه ای که .
تابع f : R → R با ضابطهٔ f ( x ) = x3 - 3x پوشا است زیرا تصویر معکوس هر عدد حقیقی مجموعه جواب معادلهٔ درجه سه x3 - 3x - y=۰ است و هر چند جمله ای درجهٔ سه با ضرایب حقیقی حداقل یک ریشهٔ حقیقی دارد. اگر چه این تابع یک به یک ( و در نتیجه دوسویی ) نیست زیرا برای مثال تصویر معکوس y = 2 مجموعهٔ { x = − 1 , x = 2 } است. ( درحقیقت، تصویر معکوس این تابع به ازای هر − 2 < = y < = 2 بیشتر از یک عضو دارد )
تابع g : R → R با ضابطهٔ g ( x ) = x² پوشا نیست زیرا هیچ عدد حقیقی مانند وجود ندارد که x² = - ۱. اگرچه تابع g : R → R n n با ضابطهٔ g ( x ) = x² ( با برد تحدید شده ) پوشا است زیرا به ازای هر از برد ( اعداد حقیقی نامنفی ) حداقل یک در دامنه ( اعداد حقیقی ) وجود دارد، به گونه ای که x² = y.
تابع لگاریتم طبیعی ln: ( 0, +∞ ) → R یک نگاشت پوشا و حتی دوسویی از مجموعهٔ اعداد حقیقی مثبت به مجموعهٔ تمام اعداد حقیقی است. وارون این تابع، تابع نمایی، پوشا نیست زیرا بردش مجموعهٔ اعداد حقیقی مثبت و دامنه اش معمولاً مجموعهٔ تمام اعداد حقیقی در نظر گرفته می شود. The matrix exponential is not surjective when seen as a map from the space of all n×n matrices to itself. It is, however, usually defined as a map from the space of all n×n matrices to the general linear group of degree n, i. e. the group of all n×n invertible matrices. Under this definition the matrix exponential is surjective for complex matrices, although still not surjective for real matrices.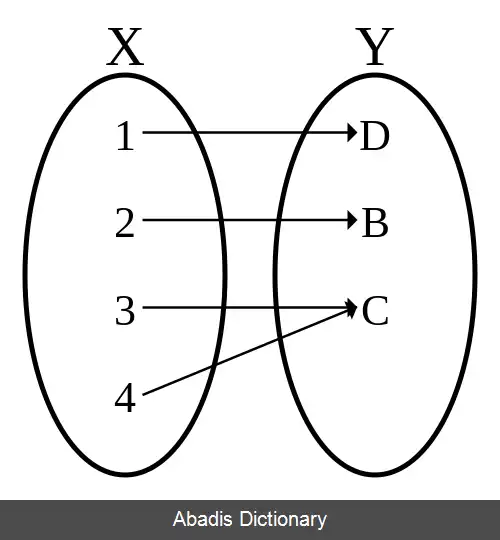
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفواژهٔ پوشا و واژه های مرتبط یک به یک و دوسویی توسط نیکلا بورباکی، تخلص گروهی از ریاضی دانان اساساً فرانسوی قرن بیستمی که کتاب های متعددی در مورد توضیح ریاضیات پیشرفته مدرن نوشتند، در سال ۱۹۳۵ معرفی شدند. واژهٔ پوشا به این معنی است که تصویر دامنهٔ تابع کاملاً برد تابع را می پوشاند.
تابع پوشا تابعی است که تصویر آن برابر بردش می باشد. یا به طور معادل تابع f با دامنهٔ و برد پوشا است اگر به ازای هر y ∈ Y وجود داشته باشد حداقل یک x ∈ X که . توابع پوشا برخی اوقات با یک پیکان راست پیما دو سر نمایش داده می شوند، مانند f: X ↠ Y.
f : X → Y ، آنگاه f پوشا است اگر
∀ y ∈ Y ; ∃ x ∈ X ; f ( x ) = y . [ ۱]
به ازای هر مجموعهٔ تابع همانی بر روی پوشا است.
تابع f : Z → { 0 , 1 } با ضابطهٔ f ( n ) = n mod 2 ( تابعی که اعداد زوج را به صفر و اعداد فرد را به یک تصویر می کند ) تابعی پوشا است.
تابع f : R → R با ضابطهٔ f ( x ) = 2 x + 1 پوشا ( و حتی دو سویی ) است، چون به ازای هر عدد حقیقی x = ( y − 1 ) / 2 ای وجود دارد به گونه ای که .
تابع f : R → R با ضابطهٔ f ( x ) = x3 - 3x پوشا است زیرا تصویر معکوس هر عدد حقیقی مجموعه جواب معادلهٔ درجه سه x3 - 3x - y=۰ است و هر چند جمله ای درجهٔ سه با ضرایب حقیقی حداقل یک ریشهٔ حقیقی دارد. اگر چه این تابع یک به یک ( و در نتیجه دوسویی ) نیست زیرا برای مثال تصویر معکوس y = 2 مجموعهٔ { x = − 1 , x = 2 } است. ( درحقیقت، تصویر معکوس این تابع به ازای هر − 2 < = y < = 2 بیشتر از یک عضو دارد )
تابع g : R → R با ضابطهٔ g ( x ) = x² پوشا نیست زیرا هیچ عدد حقیقی مانند وجود ندارد که x² = - ۱. اگرچه تابع g : R → R n n با ضابطهٔ g ( x ) = x² ( با برد تحدید شده ) پوشا است زیرا به ازای هر از برد ( اعداد حقیقی نامنفی ) حداقل یک در دامنه ( اعداد حقیقی ) وجود دارد، به گونه ای که x² = y.
تابع لگاریتم طبیعی ln: ( 0, +∞ ) → R یک نگاشت پوشا و حتی دوسویی از مجموعهٔ اعداد حقیقی مثبت به مجموعهٔ تمام اعداد حقیقی است. وارون این تابع، تابع نمایی، پوشا نیست زیرا بردش مجموعهٔ اعداد حقیقی مثبت و دامنه اش معمولاً مجموعهٔ تمام اعداد حقیقی در نظر گرفته می شود. The matrix exponential is not surjective when seen as a map from the space of all n×n matrices to itself. It is, however, usually defined as a map from the space of all n×n matrices to the general linear group of degree n, i. e. the group of all n×n invertible matrices. Under this definition the matrix exponential is surjective for complex matrices, although still not surjective for real matrices.




wiki: تابع پوشا
