در ریاضیات، تابع وایرشتراس تابعی بر خط حقیقی است که تماماً پیوسته بوده اما در هیچ نقطه ای مشتق پذیر نیست. [ ۱]
معرفی تابع وایرشتراس در سال ۱۸۷۲ میلادی دنیای ریاضیات را متحیر کرد. اهمیت این تابع از جنبهٔ تاریخی از آن رو است که مثال نقضی بود بر نظریه ای که هر تابع پیوسته را تنها در تعدادی نقطهٔ تنها نامشتق پذیر می دانست.
این تابع به نام کارل وایرشتراس که تحقیقاتی را در مورد این تابع و خصوصیاتش انجام داد و منتشر کرد نام گذاری شده است. هرچند به نظر می رسد برنهارت ریمان پیش از او به وجود این تابع اشاره کرده بوده است. [ ۲]
تابعی که وایرشتراس در مقالهٔ خود آن را معرفی کرد چنین تعریف شده است:
که در آن 0 < a < 1 ، b یک عدد صحیح فرد و a b > 1 + 3 2 π است.
به عنوان نمونه تابع f زیر دارای خاصیت تابع وایرشتراس است:[ ۳]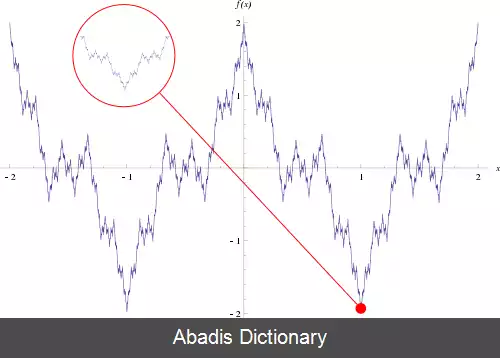
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمعرفی تابع وایرشتراس در سال ۱۸۷۲ میلادی دنیای ریاضیات را متحیر کرد. اهمیت این تابع از جنبهٔ تاریخی از آن رو است که مثال نقضی بود بر نظریه ای که هر تابع پیوسته را تنها در تعدادی نقطهٔ تنها نامشتق پذیر می دانست.
این تابع به نام کارل وایرشتراس که تحقیقاتی را در مورد این تابع و خصوصیاتش انجام داد و منتشر کرد نام گذاری شده است. هرچند به نظر می رسد برنهارت ریمان پیش از او به وجود این تابع اشاره کرده بوده است. [ ۲]
تابعی که وایرشتراس در مقالهٔ خود آن را معرفی کرد چنین تعریف شده است:
که در آن 0 < a < 1 ، b یک عدد صحیح فرد و a b > 1 + 3 2 π است.
به عنوان نمونه تابع f زیر دارای خاصیت تابع وایرشتراس است:[ ۳]


wiki: تابع وایرشتراس
