تابع وارون یا معکوس ( به انگلیسی: Inverse Function ) : در ریاضیات اگر f تابعی از مجموعه A به مجموعه B باشد، آن گاه تابع وارون ( معکوس ) f یا f−1 تابعی از B به A است، با این ویژگی که برای هر x در دامنهٔ f، نتیجه ی اعمال پی درپی تابع و وارون آن روی x، خود x خواهد بود. به دیگر سخن:[ ۱]
اگر R یک رابطه از مجموعه X به مجموعه Y باشد، آنگاه معکوس رابطه R را با R−1 نشان می دهیم که عبارت است از:
که رابطه ای از مجموعه Y به مجموعه X است. حال تابع f:X→Y نیز یک رابطه است. پس، معکوس آن را نیز می توان تعریف کرد که آن را با f−1 نشان می دهیم و حداقل یک رابطه از Y به X است.
حال این سؤال مطرح می شود که آیا f−1 همواره تابع است؟
برای این که f−1:Y→X تابع باشد، باید در شرایط تابع بودن صدق کند. یعنی
• دامنه اش همان مجموعه Y باشد؛
• هر عضو Y را به عضوی یگانه از X تصویر کند.
بنابراین معکوس تابع f:X→Y یعنی f−1 تابعی از Y به X خواهد بود اگر و فقط اگر f:X→Y یک دوسویی باشد. در این حالت f−1:Y→X را تابع معکوس تابع f می گوییم.
اگر f−1 معکوس تابع f:X→Y باشد رابطه زیر را بین دامنه و برد f و f−1 داریم:
• dom f − 1 = ran f {\displaystyle {\mbox{dom}}f^{ - 1}={\mbox{ran}}f}
• ran f − 1 = dom f {\displaystyle {\mbox{ran}}f^{ - 1}={\mbox{dom}}f}
همچنین اگر ( y=f ( x پس x, y ) ∈f ) ولذا y, x ) ∈f−1 ) پس ( x=f−1 ( y و بلعکس.
رابطه بین یک تابع و معکوسش را می توان به این صورت توصیف کرد که تابع f−1 معکوس تابع f، دقیقاً عکس تناظری که تابع f بیانگر آن است را توصیف می کند. به همین دلیل و بنابه تعریف تابع معکوس نمودار پیکانی تابع f−1 معکوس تابع f:X→Y با معکوس کردن جهت فلش ها بدست می آید.
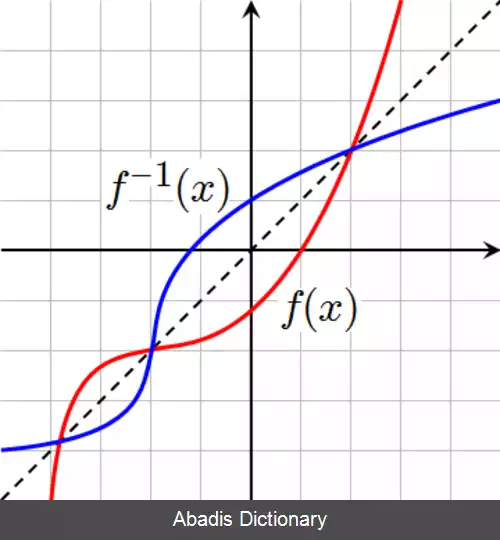
همچنین اگر f تابعی تابعی حقیقی باشد، برای اینکه نمودار معکوس f را تعیین کنیم کافی است قرینه نمودار تابع f را نسبت به نیمساز ربع اول و سوم یعنی f ( x ) =x رسم کنیم و چون انعکاس نسبت به نیمساز ربع اول و سوم موجب جابجایی مولفه های اول و دوم زوج های مرتب تابع f می شود و این در حقیقت همان هدف ماست.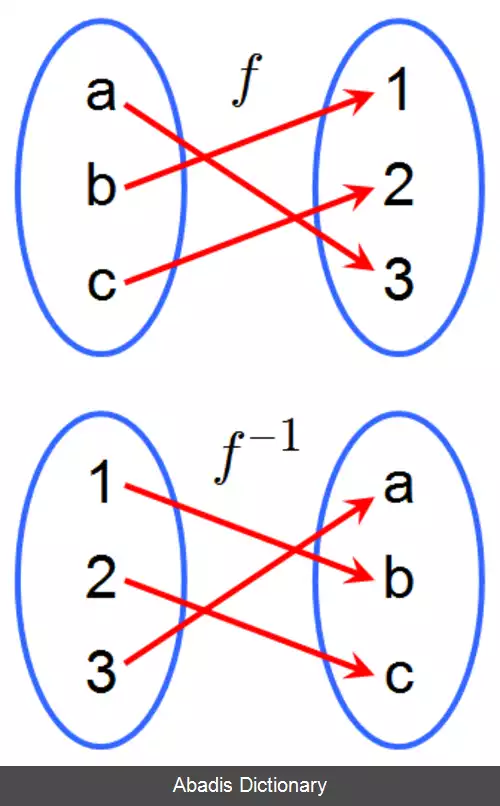
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگر R یک رابطه از مجموعه X به مجموعه Y باشد، آنگاه معکوس رابطه R را با R−1 نشان می دهیم که عبارت است از:
که رابطه ای از مجموعه Y به مجموعه X است. حال تابع f:X→Y نیز یک رابطه است. پس، معکوس آن را نیز می توان تعریف کرد که آن را با f−1 نشان می دهیم و حداقل یک رابطه از Y به X است.
حال این سؤال مطرح می شود که آیا f−1 همواره تابع است؟
برای این که f−1:Y→X تابع باشد، باید در شرایط تابع بودن صدق کند. یعنی
• دامنه اش همان مجموعه Y باشد؛
• هر عضو Y را به عضوی یگانه از X تصویر کند.
بنابراین معکوس تابع f:X→Y یعنی f−1 تابعی از Y به X خواهد بود اگر و فقط اگر f:X→Y یک دوسویی باشد. در این حالت f−1:Y→X را تابع معکوس تابع f می گوییم.
اگر f−1 معکوس تابع f:X→Y باشد رابطه زیر را بین دامنه و برد f و f−1 داریم:
• dom f − 1 = ran f {\displaystyle {\mbox{dom}}f^{ - 1}={\mbox{ran}}f}
• ran f − 1 = dom f {\displaystyle {\mbox{ran}}f^{ - 1}={\mbox{dom}}f}
همچنین اگر ( y=f ( x پس x, y ) ∈f ) ولذا y, x ) ∈f−1 ) پس ( x=f−1 ( y و بلعکس.
رابطه بین یک تابع و معکوسش را می توان به این صورت توصیف کرد که تابع f−1 معکوس تابع f، دقیقاً عکس تناظری که تابع f بیانگر آن است را توصیف می کند. به همین دلیل و بنابه تعریف تابع معکوس نمودار پیکانی تابع f−1 معکوس تابع f:X→Y با معکوس کردن جهت فلش ها بدست می آید.
همچنین اگر f تابعی تابعی حقیقی باشد، برای اینکه نمودار معکوس f را تعیین کنیم کافی است قرینه نمودار تابع f را نسبت به نیمساز ربع اول و سوم یعنی f ( x ) =x رسم کنیم و چون انعکاس نسبت به نیمساز ربع اول و سوم موجب جابجایی مولفه های اول و دوم زوج های مرتب تابع f می شود و این در حقیقت همان هدف ماست.


wiki: تابع وارون
