تابع همبستگی (مکانیک آماری). در مکانیک آماری، تابع همبستگی ( به انگلیسی: Correlation function ) معیاری برای نظم موجود در یک سیستم است. درحقیقت، توابع همبستگی چگونگی ارتباط متغیرهای میکروسکوپیک مانند اسیپن و چگالی در نقاط مختلف را توصیف می کنند. به طور ویژه، توابع همبستگی بیان کننده این هستند که به طور کمی، متغیرهای میکروسکوپیک به طور متوسط چگونه به یکدیگر در بستر فضا و زمان همبسته هستند. یک مثال کلاسیک از این دسته از توابع فضایی را در مواد فرومغناطیس و پادفرومغناطیس می توان یافت که در آن ها به ترتیب، اسپین ها ترجیح می دهند که نسبت به نزدیک ترین همسایه هایشان هم جهت یا در خلاف جهت قرار گیرند. همبستگی فضایی بین اسپین ها در چنین موادی در شکل سمت چپ نشان داده شده است.
رایج ترین تعریف از تابع همبستگی برای دو متغیر تصادفی و در مکان های و و زمان های و برابر است با متوسط هنگرد بندادی ضرب داخلی آن دو: C ( r , τ ) = ⟨ s 1 ( R , t ) ⋅ s 2 ( R + r , t + τ ) ⟩ − ⟨ s 1 ( R , t ) ⟩ ⟨ s 2 ( R + r , t + τ ) ⟩ . که در اینجا نماد براکت، ⟨ . . . ⟩ ، به معنای میانگین گیری دمایی است. بنابر قرار داد، در حوزه های مختلف علوم، علامت تابع همبستگی متفاوت است. بیشترین استفاده از تابع همبستگی برای زمانی است که s 1 و s 2 هر دو یک متغیر را توصیف کنند. به عنوان مثال، تابع همبستگی اسپین - اسپین یا تابع همبستگی مکان - مکان برای یک ذره در یک مایع یا جامد ( که معمولاً از آن با نام تابع توزیع شعاعی یا تابع همبستگی دوتایی یاد می شود ) توابع همبستگی بین یک متغیر را توابع خودهمبستگی می گویند. با این وجود در مکانیک آماری، همه توابع همبستگی، خودهمبستگی نیستند. به عنوان مثال، در فازهای چندمولفه ای چگال شده مواد، چیزی که مورد علاقه است تابع همبستگی دوتایی بین مؤلفه های مختلف است.
غالباً علاقه مند هستیم که تأثیر فضایی یک متغیر تصادفی، مثلاً جهت یک اسپین، را بر محیط پیرامونش مستقل از زمان های بعد τ . برای این منظور، در چنین مواردی، تحول زمانی سیستم را نادیده می گیریم و تعریف بالا را با τ = 0 بازنویسی می کنیم؛ بنابراین تابع همبستگی هم زمان یا فضایی C ( r , 0 ) برابر خواهد شد با:
C ( r , 0 ) = ⟨ s 1 ( R , t ) ⋅ s 2 ( R + r , t ) ⟩ − ⟨ s 1 ( R , t ) ⟩ ⟨ s 2 ( R + r , t ) ⟩ .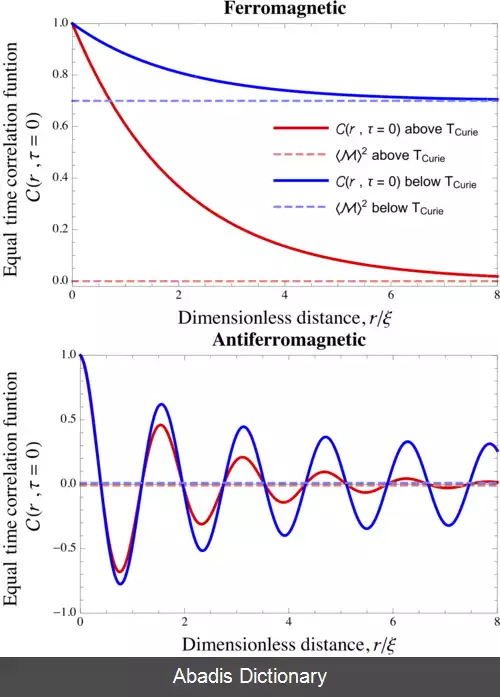
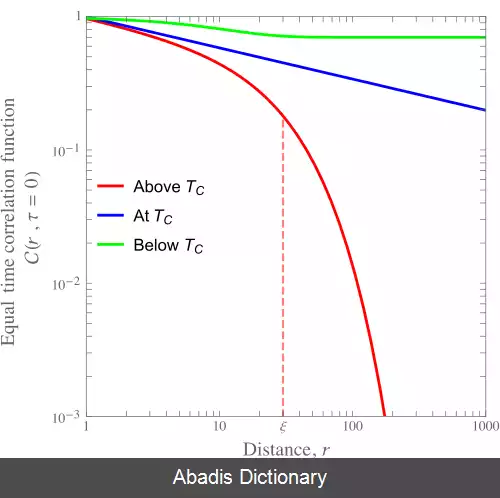
رایج ترین تعریف از تابع همبستگی برای دو متغیر تصادفی و در مکان های و و زمان های و برابر است با متوسط هنگرد بندادی ضرب داخلی آن دو: C ( r , τ ) = ⟨ s 1 ( R , t ) ⋅ s 2 ( R + r , t + τ ) ⟩ − ⟨ s 1 ( R , t ) ⟩ ⟨ s 2 ( R + r , t + τ ) ⟩ . که در اینجا نماد براکت، ⟨ . . . ⟩ ، به معنای میانگین گیری دمایی است. بنابر قرار داد، در حوزه های مختلف علوم، علامت تابع همبستگی متفاوت است. بیشترین استفاده از تابع همبستگی برای زمانی است که s 1 و s 2 هر دو یک متغیر را توصیف کنند. به عنوان مثال، تابع همبستگی اسپین - اسپین یا تابع همبستگی مکان - مکان برای یک ذره در یک مایع یا جامد ( که معمولاً از آن با نام تابع توزیع شعاعی یا تابع همبستگی دوتایی یاد می شود ) توابع همبستگی بین یک متغیر را توابع خودهمبستگی می گویند. با این وجود در مکانیک آماری، همه توابع همبستگی، خودهمبستگی نیستند. به عنوان مثال، در فازهای چندمولفه ای چگال شده مواد، چیزی که مورد علاقه است تابع همبستگی دوتایی بین مؤلفه های مختلف است.
غالباً علاقه مند هستیم که تأثیر فضایی یک متغیر تصادفی، مثلاً جهت یک اسپین، را بر محیط پیرامونش مستقل از زمان های بعد τ . برای این منظور، در چنین مواردی، تحول زمانی سیستم را نادیده می گیریم و تعریف بالا را با τ = 0 بازنویسی می کنیم؛ بنابراین تابع همبستگی هم زمان یا فضایی C ( r , 0 ) برابر خواهد شد با:
C ( r , 0 ) = ⟨ s 1 ( R , t ) ⋅ s 2 ( R + r , t ) ⟩ − ⟨ s 1 ( R , t ) ⟩ ⟨ s 2 ( R + r , t ) ⟩ .


تابع همبستگی (نجوم). در نجوم، تابع همبستگی توزیع کهکشان ها در کیهان را توصیف می کند. بر اساس مشاهدات، توزیع کهکشان ها در آسمان، یکنواخت نیست و آن ها در ساختارهایی مانند خوشه ها، ابرخوشه ها، رشته ها، تهی جاها و … وجود دارند. عدم یکنواختی این توزیع، به کمک تابع همبستگی دو - نقطه ای توصیف می شود.
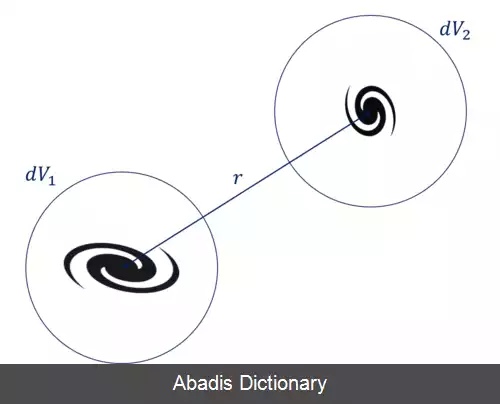
تابع همبستگی دونقطه ای، ξ ( r ) ، فزونی احتمال پیدا کردن دو کهکشان در فاصلهٔ r نسبت به توزیع یکنواخت است. به عبارت دیگر، احتمال پیدا کردن دو کهکشان در فاصلهٔ ξ ( r ) از یک دیگر، نسبت به حالتی که توزیع کهکشان ها یکنواخت باشد، چه قدر افزایش خواهد یافت. به بیان ریاضی:[ ۱]
d P = n d V
که در آن n چگالی تعداد میانگین کهکشان ها، r طول همراه و d P احتمال فزونی است. در منابع نجومی، از تعریف زیر که توسط پیبلز ارائه شده است، استفاده می شود.
برای یک توزیع کاملاً تصادفی، ξ ( r ) = 0 . مقادیر مثبت نشان دهندهٔ شکل گیری خوشه و مقادیر منفی نشان دهندهٔ معمولی بودن هستند. این تعریف با فرض همگنی و همسانگردی انجام شده است. در غیر این صورت ξ ( r ) تابعیت برداری خواهد داشت.
در ابعاد کوچک ( 0. 1 h − 1 M p c < r < 10 h − 1 M p c ) ، تابع همبستگی به شکل توانی ξ ( r ) = ( r 0 r ) γ است که در آن شیب γ ≈ 1. 8 و طول همبستگی r 0 ≈ 5 h − 1 M p c است. [ ۲]
تابع همبستگی، انواع مختلفی دارد ( ۲ بعدی یا ۳ بعدی، فضایی یا زاویه ای ) .
ارتباط بین طیف توان و تابع همبستگی، از طریق تبدیل فوریه امکان پذیر است:
ξ ( r ) = 1 2 π 2 ∫ d k k 2 P ( k ) sin ( k r ) k r
به عبارت دیگر، تابع همبستگی، طیف توان توزیع کهکشان ها در دامنه فرکانس است. طیف توان مستقیماً توسط نظریه های تشکیل ساختار پیش بینی می شود و توصیف آماری کاملی از افت و خیزها ارائه می دهد.
تابع همبستگی nنقطه ای به ازای nهای بزرگ تر از ۲ ( به انگلیسی: Cross - correlation ) به شکل مشابهی تعریف می شود.
برای اندازه گیری ξ ( r ) در یک نمونهٔ رصدی از کهکشان ها، ابتدا باید نمونه ای تصادفی از کهکشان ها ساخته شود که از لحاظ ابعاد، عیناً ویژگی های نمونهٔ رصدی را دارد. مقدار تابع همبستگی برابر است با:
1 + ξ = n R n D D D D R
D D و D R به ترتیب تعداد جفت های کهکشان دارای فاصلهٔ در نمونهٔ رصدی و مجموع نمونهٔ تصادفی و رصدی هستند. n D و n R نیز چگالی تعداد میانگین در همان نمونه ها هستند.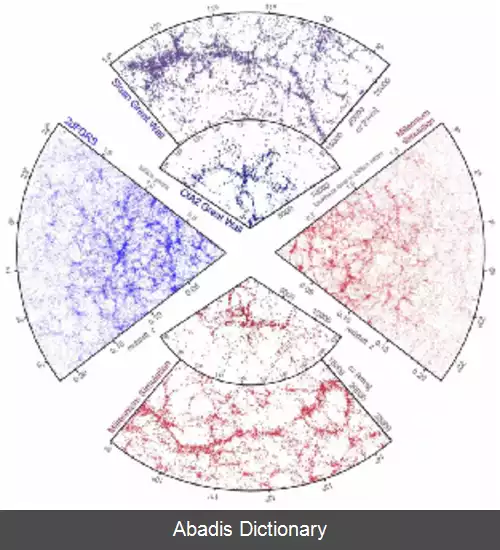

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتابع همبستگی دونقطه ای، ξ ( r ) ، فزونی احتمال پیدا کردن دو کهکشان در فاصلهٔ r نسبت به توزیع یکنواخت است. به عبارت دیگر، احتمال پیدا کردن دو کهکشان در فاصلهٔ ξ ( r ) از یک دیگر، نسبت به حالتی که توزیع کهکشان ها یکنواخت باشد، چه قدر افزایش خواهد یافت. به بیان ریاضی:[ ۱]
d P = n d V
که در آن n چگالی تعداد میانگین کهکشان ها، r طول همراه و d P احتمال فزونی است. در منابع نجومی، از تعریف زیر که توسط پیبلز ارائه شده است، استفاده می شود.
برای یک توزیع کاملاً تصادفی، ξ ( r ) = 0 . مقادیر مثبت نشان دهندهٔ شکل گیری خوشه و مقادیر منفی نشان دهندهٔ معمولی بودن هستند. این تعریف با فرض همگنی و همسانگردی انجام شده است. در غیر این صورت ξ ( r ) تابعیت برداری خواهد داشت.
در ابعاد کوچک ( 0. 1 h − 1 M p c < r < 10 h − 1 M p c ) ، تابع همبستگی به شکل توانی ξ ( r ) = ( r 0 r ) γ است که در آن شیب γ ≈ 1. 8 و طول همبستگی r 0 ≈ 5 h − 1 M p c است. [ ۲]
تابع همبستگی، انواع مختلفی دارد ( ۲ بعدی یا ۳ بعدی، فضایی یا زاویه ای ) .
ارتباط بین طیف توان و تابع همبستگی، از طریق تبدیل فوریه امکان پذیر است:
ξ ( r ) = 1 2 π 2 ∫ d k k 2 P ( k ) sin ( k r ) k r
به عبارت دیگر، تابع همبستگی، طیف توان توزیع کهکشان ها در دامنه فرکانس است. طیف توان مستقیماً توسط نظریه های تشکیل ساختار پیش بینی می شود و توصیف آماری کاملی از افت و خیزها ارائه می دهد.
تابع همبستگی nنقطه ای به ازای nهای بزرگ تر از ۲ ( به انگلیسی: Cross - correlation ) به شکل مشابهی تعریف می شود.
برای اندازه گیری ξ ( r ) در یک نمونهٔ رصدی از کهکشان ها، ابتدا باید نمونه ای تصادفی از کهکشان ها ساخته شود که از لحاظ ابعاد، عیناً ویژگی های نمونهٔ رصدی را دارد. مقدار تابع همبستگی برابر است با:
1 + ξ = n R n D D D D R
D D و D R به ترتیب تعداد جفت های کهکشان دارای فاصلهٔ در نمونهٔ رصدی و مجموع نمونهٔ تصادفی و رصدی هستند. n D و n R نیز چگالی تعداد میانگین در همان نمونه ها هستند.



wiki: تابع همبستگی (نجوم)
