تابع نمایی کشیده ( به انگلیسی: Stretched exponential function ) که به این صورت تعریف می شود:
f β ( t ) = e − t β
با قرار دادن یک توزیع توانی کسری در یک تابع نمایی به دست می آید. در بیشتر کاربردها، این تابع فقط برای شناسه ( آرگومان ) t بین ۰ و +∞ معنی دار است. با β = ۱ تابع نمایی معمولی بازیابی می شود. هنگامیکه نمای کشیدگی β بین ۰ و ۱ قرار دارد، گراف log f دربرابر t به صورت مشخصه ای کشیده می شود، و نام تابع از این موضوع گرفته شده است. تابع نمایی فشرده ( با β> ۱ ) دارای اهمیت کاربردی کمتری است، اما یک استثنا وجود دارد که آن β = ۲ است، و توزیع نرمال به دست می دهد.
در ریاضیات، به نمایی کشیده، توزیع ویبول تجمعی مکمل نیز می گویند. نمایی کشیده همچنین تابع مشخصه، در اصل تبدیل فوریه، برای توزیع ایستا - آلفا متقارن لیوی می باشد.
در فیزیک، از تابع نمایی کشیده به عنوان توصیف پدیدارشناختی واهلش در سامانه های بی نظم استفاده می شود. این تابع اولین بار توسط رودولف کلراوش در سال ۱۸۵۴ برای توصیف تخلیه الکتریکی یک خازن معرفی شد؛[ ۱] از این رو به آن تابع کلراوش هم می گویند. در سال ۱۹۷۰، جی. ویلیامز و دی. سی. واتس از تبدیل فوریهٔ نمایی کشیده استفاده کردند تا طیف های دی الکتریک پلیمرها را توصیف کنند؛[ ۲] در این زمینه، نمایی کشیده یا تبدیل فوریه آن، تابع کهلراوش – ویلیامز – وات ( KWW ) هم نام دارد.
در کاربردهای پدیدارشناسانه، این موضوع مشخص نیست که آیا از تابع نمایی کشیده، یا برای توصیف تابع توزیع دیفرانسیل یا توزیع انتگرال استفاده شود، یا برای هیچ کدام. در هر حالت، به زوال مجانبی مشابهی می رسیم، اما پیش فاکتور توزیع توانی آن متفاوت است، که سازگاری را مبهم تر از توانی های ساده می کند. در حالت های خاص، [ ۳] [ ۴] [ ۵] [ ۶] می توان نشان داد که زوال مجانبی یک نمای کشیده است، اما پیش فاکتور معمولاً یک توان بی ربط است.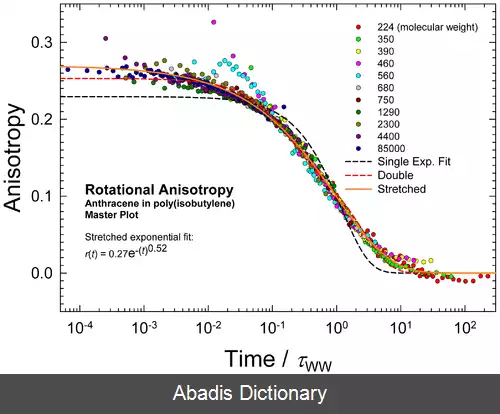
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفf β ( t ) = e − t β
با قرار دادن یک توزیع توانی کسری در یک تابع نمایی به دست می آید. در بیشتر کاربردها، این تابع فقط برای شناسه ( آرگومان ) t بین ۰ و +∞ معنی دار است. با β = ۱ تابع نمایی معمولی بازیابی می شود. هنگامیکه نمای کشیدگی β بین ۰ و ۱ قرار دارد، گراف log f دربرابر t به صورت مشخصه ای کشیده می شود، و نام تابع از این موضوع گرفته شده است. تابع نمایی فشرده ( با β> ۱ ) دارای اهمیت کاربردی کمتری است، اما یک استثنا وجود دارد که آن β = ۲ است، و توزیع نرمال به دست می دهد.
در ریاضیات، به نمایی کشیده، توزیع ویبول تجمعی مکمل نیز می گویند. نمایی کشیده همچنین تابع مشخصه، در اصل تبدیل فوریه، برای توزیع ایستا - آلفا متقارن لیوی می باشد.
در فیزیک، از تابع نمایی کشیده به عنوان توصیف پدیدارشناختی واهلش در سامانه های بی نظم استفاده می شود. این تابع اولین بار توسط رودولف کلراوش در سال ۱۸۵۴ برای توصیف تخلیه الکتریکی یک خازن معرفی شد؛[ ۱] از این رو به آن تابع کلراوش هم می گویند. در سال ۱۹۷۰، جی. ویلیامز و دی. سی. واتس از تبدیل فوریهٔ نمایی کشیده استفاده کردند تا طیف های دی الکتریک پلیمرها را توصیف کنند؛[ ۲] در این زمینه، نمایی کشیده یا تبدیل فوریه آن، تابع کهلراوش – ویلیامز – وات ( KWW ) هم نام دارد.
در کاربردهای پدیدارشناسانه، این موضوع مشخص نیست که آیا از تابع نمایی کشیده، یا برای توصیف تابع توزیع دیفرانسیل یا توزیع انتگرال استفاده شود، یا برای هیچ کدام. در هر حالت، به زوال مجانبی مشابهی می رسیم، اما پیش فاکتور توزیع توانی آن متفاوت است، که سازگاری را مبهم تر از توانی های ساده می کند. در حالت های خاص، [ ۳] [ ۴] [ ۵] [ ۶] می توان نشان داد که زوال مجانبی یک نمای کشیده است، اما پیش فاکتور معمولاً یک توان بی ربط است.

wiki: تابع نمایی کشیده
